24 Theorems about triangles

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

In geometry, Apollonius's theorem is a theorem relating the length of a median of a triangle to the lengths of its sides. It states that "the sum of the squares of any two sides of any triangle equals twice the square on half the third side, together with twice the square on the median bisecting the third side".

Bottema's theorem is a theorem in plane geometry by the Dutch mathematician Oene Bottema.

Carnot's theorem describes a relation between conic sections and triangles.

Carnot's theorem describes a necessary and sufficient condition for a common point of intersection of three lines being perpendicular to the (extended) sides of triangle. The theorem can also be thought of as a generalisation of the Pythagorean theorem

Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O, to meet opposite sides at D, E and F respectively. Then, using signed lengths of segments,

In projective geometry, Desargues's theorem, named after Girard Desargues, states:Two triangles are in perspective axially if and only if they are in perspective centrally.

In Euclidean geometry, the Droz-Farny line theorem is a property of two perpendicular lines through the orthocenter of an arbitrary triangle.

In geometry, Heron's formula, named after Hero of Alexandria, gives the area of a triangle when the length of all three sides are known. Unlike other triangle area formulae, there is no need to calculate angles or other distances in the triangle first.

In geometry, the hinge theorem states that if two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle. This theorem is actually Propositions 24 of Book 1 of Euclid's Elements. The theorem states the following:If two sides of one triangle are congruent, respectively, to two sides of a second triangle, and the included angle of the first triangle is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second.

In plane geometry, a Jacobi point is a point in the Euclidean plane determined by a triangle ABC and a triple of angles α, β, and γ. This information is sufficient to determine three points X, Y, and Z such that ∠ZAB = ∠YAC = α, ∠XBC = ∠ZBA = β, and ∠YCA = ∠XCB = γ. Then, by a theorem of Karl Friedrich Andreas Jacobi, the lines AX, BY, and CZ are concurrent, at a point N called the Jacobi point.

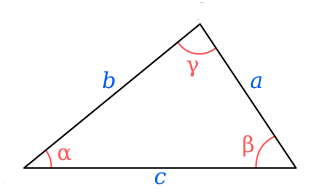
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. According to the law,

In trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.

In mathematics, Marden's theorem, named after Morris Marden but proved about 100 years earlier by Jörg Siebeck, gives a geometric relationship between the zeroes of a third-degree polynomial with complex coefficients and the zeroes of its derivative. See also geometrical properties of polynomial roots.

Maxwell's theorem is the following statement about triangles in the plane.For a given triangle and a point not on the sides of that triangle construct a second triangle , such that the side is parallel to the line segment , the side is parallel to the line segment and the side is parallel to the line segment . Then the parallel to through , the parallel to through and the parallel to through intersect in a common point .

Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC, and AB at points D, E, and F respectively, with D, E, and F distinct from A, B, and C, then

In trigonometry, Mollweide's formula, sometimes referred to in older texts as Mollweide's equations, named after Karl Mollweide, is a set of two relationships between sides and angles in a triangle.

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all of the trisectors are intersected, one obtains four other equilateral triangles.

In geometry, Napoleon's theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those equilateral triangles themselves form an equilateral triangle.

Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.

In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the pairwise intersections of three cevians. The theorem states that if in triangle points , , and lie on segments , , and , then writing , , and , the signed area of the triangle formed by the cevians , , and is the area of triangle times

Sylvester's theorem or Sylvester's formula describes a particular interpretation of the sum of three pairwise distinct vectors of equal length in the context of triangle geometry. It is also referred to as Sylvester's (triangle) problem in literature, when it is given as a problem rather than a theorem. The theorem is named after the British mathematician James Joseph Sylvester.

Thomsen's theorem, named after Gerhard Thomsen, is a theorem in elementary geometry. It shows that a certain path constructed by line segments being parallel to the edges of a triangle always ends up at its starting point.