25 Applied mathematics

Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models.

Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.

In data visualization, an Andrews plot or Andrews curve is a way to visualize structure in high-dimensional data. It is basically a rolled-down, non-integer version of the Kent–Kiviat radar m chart, or a smoothed version of a parallel coordinate plot. It is named after the statistician David F. Andrews.

Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models.

In geometry and linear algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from one such basis to another is through an orthogonal transformation.

Computational mathematics involves mathematical research in mathematics as well as in areas of science where computing plays a central and essential role, and emphasizes algorithms, numerical methods, and symbolic computations.

Cryptanalysis is the study of analyzing information systems in order to study the hidden aspects of the systems. Cryptanalysis is used to breach cryptographic security systems and gain access to the contents of encrypted messages, even if the cryptographic key is unknown.

Cryptography, or cryptology, is the practice and study of techniques for secure communication in the presence of third parties called adversaries. More generally, cryptography is about constructing and analyzing protocols that prevent third parties or the public from reading private messages; various aspects in information security such as data confidentiality, data integrity, authentication, and non-repudiation are central to modern cryptography. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, electrical engineering, communication science, and physics. Applications of cryptography include electronic commerce, chip-based payment cards, digital currencies, computer passwords, and military communications.

Discrete tomography focuses on the problem of reconstruction of binary images from a small number of their projections.

In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers. Dichotomization is the special case of discretization in which the number of discrete classes is 2, which can approximate a continuous variable as a binary variable.

In the statistical theory of estimation, the German tank problem consists of estimating the maximum of a discrete uniform distribution from sampling without replacement. In simple terms, suppose there exists an unknown number of items which are sequentially numbered from 1 to N. A random sample of these items is taken and their sequence numbers observed; the problem is to estimate N from these observed numbers.

In bioinformatics, k-mers are subsequences of length contained within a biological sequence. Primarily used within the context of computational genomics and sequence analysis, in which k-mers are composed of nucleotides, k-mers are capitalized upon to assemble DNA sequences, improve heterologous gene expression, identify species in metagenomic samples, and create attenuated vaccines. Usually, the term k-mer refers to all of a sequence's subsequences of length , such that the sequence AGAT would have four monomers, three 2-mers, two 3-mers and one 4-mer (AGAT). More generally, a sequence of length will have k-mers and total possible k-mers, where is number of possible monomers.

Mathematical Magick is a treatise by the English clergyman, natural philosopher, polymath and author John Wilkins. It was first published in 1648 in London, another edition was printed in 1680 and further editions were published in 1691 and 1707.

Mathematical sociology is the area of sociology that uses mathematics to construct social theories. Mathematical sociology aims to take sociological theory and to express it in mathematical terms. The benefits of this approach include increased clarity and the ability to use mathematics to derive implications of a theory that cannot be arrived at intuitively. In mathematical sociology, the preferred style is encapsulated in the phrase "constructing a mathematical model." This means making specified assumptions about some social phenomenon, expressing them in formal mathematics, and providing an empirical interpretation for the ideas. It also means deducing properties of the model and comparing these with relevant empirical data. Social network analysis is the best-known contribution of this subfield to sociology as a whole and to the scientific community at large. The models typically used in mathematical sociology allow sociologists to understand how predictable local interactions are and they are often able to elicit global patterns of social structure.

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

The Research, Innovation, and Dissemination Center for Neuromathematics is a Brazilian research center established in 2013 at the University of São Paulo that is dedicated to integrating mathematical modeling and theoretical neuroscience. Among the core missions of NeuroMat are the creation of a new mathematical system to understanding neural data and the development of neuroscientific open-source computational tools, keeping an active role under the context of open knowledge, open science and scientific dissemination. The research center is headed by Antonio Galves, from USP's Institute of Mathematics and Statistics, and is funded by the São Paulo Research Foundation (FAPESP). As of 2019, the co-principal investigators are Oswaldo Baffa Filho (USP), Pablo A. Ferrari (USP/UBA), Fernando da Paixão (UNICAMP), Antonio Carlos Roque (USP), Jorge Stolfi (UNICAMP), and Cláudia D. Vargas (UFRJ). Ernst W. Hamburger (USP) was the former director of scientific dissemination. NeuroMat's International Advisory Board consists of David R. Brillinger, Leonardo G. Cohen (NIH), Markus Diesmann (Jülich), Francesco Guerra, Wojciech Szpankowski (Purdue).

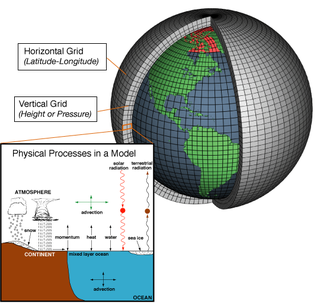
Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic results. A number of global and regional forecast models are run in different countries worldwide, using current weather observations relayed from radiosondes, weather satellites and other observing systems as inputs.

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. As with the rest of analytical mechanics, Routhian mechanics is completely equivalent to Newtonian mechanics, all other formulations of classical mechanics, and introduces no new physics. It offers an alternative way to solve mechanical problems.

In mathematics and its applications, the signed distance function of a set Ω in a metric space determines the distance of a given point x from the boundary of Ω, with the sign determined by whether x is in Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead.

In geometry, a spirangle is a figure related to a spiral. Spirangles are similar to spirals in that they expand from a center point as they grow larger, but they are made out of straight line segments, instead of curves. Spirangle vectographs are used in vision therapy to promote stereopsis and help resolve problems with hand–eye coordination.

Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models.

In applied statistics, total least squares is a type of errors-in-variables regression, a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account. It is a generalization of Deming regression and also of orthogonal regression, and can be applied to both linear and non-linear models.

Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. The word comes from Latin vibrationem. The oscillations may be periodic, such as the motion of a pendulum—or random, such as the movement of a tire on a gravel road.

Vflo is a commercially available, physics-based distributed hydrologic model generated by Vieux & Associates, Inc. Vflo uses radar rainfall data for hydrologic input to simulate distributed runoff. Vflo employs GIS maps for parameterization via a desktop interface. The model is suited for distributed hydrologic forecasting in post-analysis and in continuous operations. Vflo output is in the form of hydrographs at selected drainage network grids, as well as distributed runoff maps covering the watershed. Model applications include civil infrastructure operations and maintenance, stormwater prediction and emergency management, continuous and short-term surface water runoff, recharge estimation, soil moisture monitoring, land use planning, water quality monitoring, and water resources management.