26 Area

Area is the quantity that expresses the extent of a two-dimensional figure or shape or planar lamina, in the plane. Surface area is its analog on the two-dimensional surface of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve or the volume of a solid.

In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In geometry, a base is a side of a polygon or a face of a polyhedron, particularly one oriented perpendicular to the direction in which height is measured, or on what is considered to be the "bottom" of the figure. This term is commonly applied to triangles, parallelograms, trapezoids, cylinders, cones, pyramids, parallelepipeds and frustums.

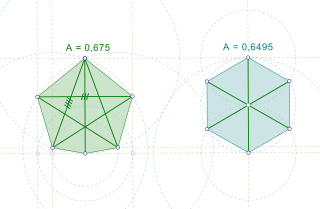
In geometry, the biggest little polygon for a number n is the n-sided polygon that has diameter one and that has the largest area among all diameter-one n-gons. One non-unique solution when n = 4 is a square, and the solution is a regular polygon when n is an odd number, but the solution is irregular otherwise.

In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it is also known as the Blaschke–Lebesgue inequality. It is named after Wilhelm Blaschke and Henri Lebesgue, who published it separately in the early 20th century.

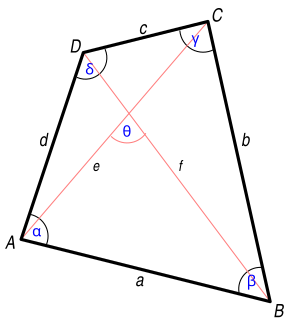
In geometry, Bretschneider's formula is the following expression for the area of a general quadrilateral:

In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. 3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes.

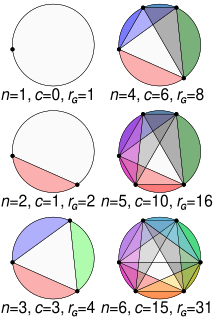
In geometry, the problem of dividing a circle into areas by means of an inscribed polygon with n sides in such a way as to maximise the number of areas created by the edges and diagonals, sometimes called Moser's circle problem, has a solution by an inductive method. The greatest possible number of regions, rG = + + 1, giving the sequence 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, .... Though the first five terms match the geometric progression 2n − 1, it diverges at n = 6, showing the risk of generalising from only a few observations.

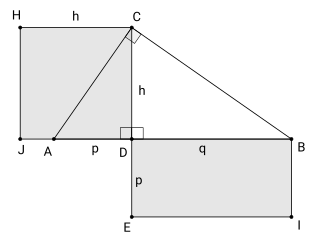
The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the lengths of the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.

In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points within a region in the plane, in order to avoid triangles of small area. It is named after Hans Heilbronn, who conjectured prior to 1950 that this smallest triangle area is necessarily at most inversely proportional to the square of the number of points. Heilbronn's conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

In geometry, Heron's formula, named after Hero of Alexandria, gives the area of a triangle when the length of all three sides are known. Unlike other triangle area formulae, there is no need to calculate angles or other distances in the triangle first.

The earliest recorded systems of weights and measures originate in the 3rd or 4th millennium BC. Even the very earliest civilizations needed measurement for purposes of agriculture, construction, and trade. Early standard units might only have applied to a single community or small region, with every area developing its own standards for lengths, areas, volumes and masses. Often such systems were closely tied to one field of use, so that volume measures used, for example, for dry grains were unrelated to those for liquids, with neither bearing any particular relationship to units of length used for measuring cloth or land. With development of manufacturing technologies, and the growing importance of trade between communities and ultimately across the Earth, standardized weights and measures became critical. Starting in the 18th century, modernized, simplified and uniform systems of weights and measures were developed, with the fundamental units defined by ever more precise methods in the science of metrology. The discovery and application of electricity was one factor motivating the development of standardized internationally applicable units.

A hyperbolic sector is a region of the Cartesian plane {(x,y)} bounded by rays from the origin to two points and and by the rectangular hyperbola xy = 1.

In plane geometry, a triangle ABC contains a triangle having one-seventh of the area of ABC, which is formed as follows: the sides of this triangle lie on cevians p, q, r wherep connects A to a point on BC that is one-third the distance from B to C, q connects B to a point on CA that is one-third the distance from C to A, r connects C to a point on AB that is one-third the distance from A to B.

Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.

In mathematics, Pappus's centroid theorem is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution.

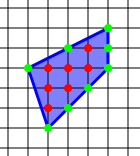
Given a simple polygon constructed on a grid of equal-distanced points such that all the polygon's vertices are grid points, Pick's theorem provides a simple formula for calculating the area A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the number b of lattice points on the boundary placed on the polygon's perimeter:

In elementary geometry, the pizza theorem states the equality of two areas that arise when one partitions a disk in a certain way.

In mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:

The quadratrix or trisectrix of Hippias is a curve, which is created by a uniform motion. It is one of the oldest examples for a kinematic curve, that is a curve created through motion. Its discovery is attributed to the Greek sophist Hippias of Elis, who used it around 420 BC in an attempt to solve the angle trisection problem. Later around 350 BC Dinostratus used it in an attempt to solve the problem of squaring the circle.

In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the pairwise intersections of three cevians. The theorem states that if in triangle points , , and lie on segments , , and , then writing , , and , the signed area of the triangle formed by the cevians , , and is the area of triangle times

The shoelace formula or shoelace algorithm is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane. The user cross-multiplies corresponding coordinates to find the area encompassing the polygon, and subtracts it from the surrounding polygon to find the area of the polygon within. It is called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like threading shoelaces. It is also sometimes called the shoelace method. It has applications in surveying and forestry, among other areas.

In geometry, a square trisection consists of cutting a square into pieces that can be rearranged to form three identical squares.

The square–cube law is a mathematical principle, applied in a variety of scientific fields, which describes the relationship between the volume and the surface area as a shape's size increases or decreases. It was first described in 1638 by Galileo Galilei in his Two New Sciences as the "...ratio of two volumes is greater than the ratio of their surfaces".

The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra, for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration.

In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate a scalar field over the surface, or a vector field. If a region R is not flat, then it is called a surface as shown in the illustration.