26 Multi dimensional geometry

In mathematics, a convex body in n-dimensional Euclidean space is a compact convex set with non-empty interior.

In geometry, a cross-polytope, hyperoctahedron, orthoplex, or cocube is a regular, convex polytope that exists in n-dimensions. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.

In geometry, demihypercubes are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγn for being half of the hypercube family, γn. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n (n-1)-demicubes, and 2n (n-1)-simplex facets are formed in place of the deleted vertices.

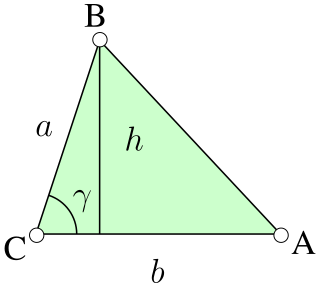
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.

A five-dimensional space is a space with five dimensions. If interpreted physically, that is one more than the usual three spatial dimensions and the fourth dimension of time used in relativistic physics. It is an abstraction which occurs frequently in mathematics, where it is a legitimate construct. In physics and mathematics, a sequence of N numbers can be understood to represent a location in an N-dimensional space. Whether or not the universe is five-dimensional is a topic of debate.

A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height.

New possibilities opened up by the concept of four-dimensional space helped inspire many modern artists in the first half of the twentieth century. Early Cubists, Surrealists, Futurists, and abstract artists took ideas from higher-dimensional mathematics and used them to radically advance their work.

In musical tuning systems, the hexany, invented by Erv Wilson, represents one of the simplest structures found in his Combination Product Sets.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space and m-planes are represented by the intersections of the (m+1)-planes in Minkowski space with S+. The hyperbolic distance function admits a simple expression in this model. The hyperboloid model of the n-dimensional hyperbolic space is closely related to the Beltrami–Klein model and to the Poincaré disk model as they are projective models in the sense that the isometry group is a subgroup of the projective group.

In geometry, a hypercone is the figure in the 4-dimensional Euclidean space represented by the equation

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .

In geometry, an n-orthotope is the generalization of a rectangle for higher dimensions, formally defined as the Cartesian product of intervals.

In geometry of higher dimensions, a hypersphere is the set of points at a constant distance from a given point called its centre. It is a manifold of codimension one—that is, with one dimension less than that of the ambient space.

In mathematics, the John ellipsoid or Löwner-John ellipsoid E(K) associated to a convex body K in n-dimensional Euclidean space Rn can refer to the n-dimensional ellipsoid of maximal volume contained within K or the ellipsoid of minimal volume that contains K.

This page lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces.

The Rubik's Cube is the original and best known of the three-dimensional sequential move puzzles. There have been many virtual implementations of this puzzle in software. It is a natural extension to create sequential move puzzles in more than three dimensions. Although no such puzzle could ever be physically constructed, the rules of how they operate are quite rigorously defined mathematically and are analogous to the rules found in three-dimensional geometry. Hence, they can be simulated by software. As with the mechanical sequential move puzzles, there are records for solvers, although not yet the same degree of competitive organisation.

In mathematics, an n-sphere is a topological space that is homeomorphic to a standard n-sphere, which is the set of points in (n + 1)-dimensional Euclidean space that are situated at a constant distance r from a fixed point, called the center. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit n-sphere or simply the n-sphere for brevity. In terms of the standard norm, the n-sphere is defined as

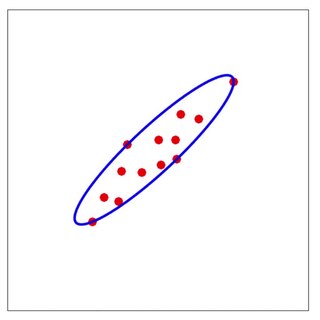
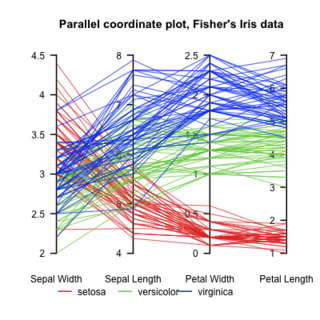
Parallel coordinates are a common way of visualizing and analyzing high-dimensional datasets.

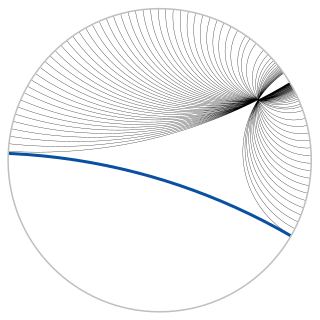
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which the points of the geometry are inside the unit disk, and the straight lines consist of all circular arcs contained within that disk that are orthogonal to the boundary of the disk, plus all diameters of the disk.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given space.

In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries gravitational force. Thus string theory is a theory of quantum gravity.

Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.

In geometry, a transversal plane is a plane that intersects two or more lines or planes. A transversal plane may also form dihedral angles.

Two-dimensional space is a geometric setting in which two values are required to determine the position of an element. The set ℝ2 of pairs of real numbers with appropriate structure often serves as the canonical example of a two-dimensional Euclidean space. For a generalization of the concept, see dimension.

In geometry, a ball is a region in space comprising all points within a fixed distance from a given point; that is, it is the region enclosed by a sphere or hypersphere. An n-ball is a ball in n-dimensional Euclidean space. The volume of a unit n-ball is an important expression that occurs in formulas throughout mathematics; it generalizes the notion of the volume enclosed by a sphere in 3-dimensional space.