 W
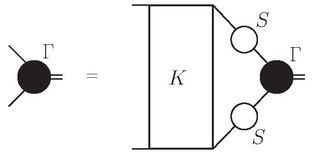
WThe Bethe–Salpeter equation describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
 W
WThe Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium, devised by Ludwig Boltzmann in 1872. The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.
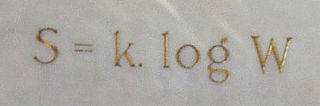 W
WIn statistical mechanics, Boltzmann's equation is a probability equation relating the entropy , also written as , of an ideal gas to the quantity , the number of real microstates corresponding to the gas's macrostate:
 W
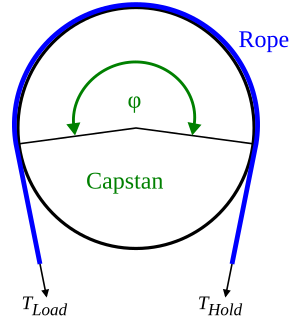
WThe capstan equation or belt friction equation, also known as Eytelwein's formula, relates the hold-force to the load-force if a flexible line is wound around a cylinder.
 W
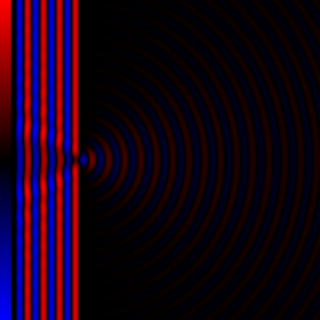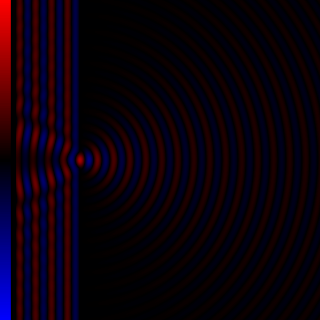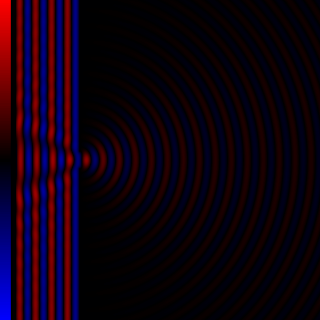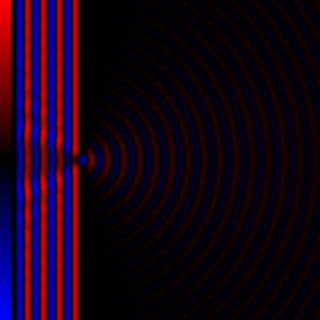
WDiffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations.
 W
WIn the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the phase velocity and group velocity of waves in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency dependence of wave propagation and attenuation.
 W
WIn the general theory of relativity the Einstein field equations relate the geometry of spacetime to the distribution of matter within it.
 W
WIn astrophysics, the Emden–Chandrasekhar equation is a dimensionless form of the Poisson equation for the density distribution of a spherically symmetric isothermal gas sphere subjected to its own gravitational force, named after Robert Emden and Subrahmanyan Chandrasekhar. The equation was first introduced by Robert Emden in 1907. The equation reads
 W
WIn physics and thermodynamics, an equation of state is a thermodynamic equation relating state variables which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature (PVT), or internal energy. Equations of state are useful in describing the properties of fluids, mixtures of fluids, solids, and the interior of stars.
 W
WIn physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behaviour of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.
 W
WIn fluid dynamics, the Euler equations are a set of quasilinear hyperbolic equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. The equations represent Cauchy equations of conservation of mass (continuity), and balance of momentum and energy, and can be seen as particular Navier–Stokes equations with zero viscosity and zero thermal conductivity. In fact, Euler equations can be obtained by linearization of some more precise continuity equations like Navier–Stokes equations in a local equilibrium state given by a Maxwellian. The Euler equations can be applied to incompressible and to compressible flow – assuming the flow velocity is a solenoidal field, or using another appropriate energy equation respectively. Historically, only the incompressible equations have been derived by Euler. However, fluid dynamics literature often refers to the full set – including the energy equation – of the more general compressible equations together as "the Euler equations".
 W
WThe first law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic processes, distinguishing two kinds of transfer of energy, as heat and as thermodynamic work, and relating them to a function of a body's state, called Internal energy.
 W
WThe Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, even though no one realized that the "vibrations" of the wave were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.
 W
WIn electrodynamics, the Larmor formula is used to calculate the total power radiated by a non relativistic point charge as it accelerates. It was first derived by J. J. Larmor in 1897, in the context of the wave theory of light.
 W
WThis article summarizes equations in the theory of electromagnetism.
 W
WThis article summarizes equations in the theory of nuclear physics and particle physics.
 W
WThe study of electromagnetism in higher education, as a fundamental part of both physics and engineering, is typically accompanied by textbooks devoted to the subject. The American Physical Society and the American Association of Physics Teachers recommend a full year of graduate study in electromagnetism for all physics graduate students. A joint task force by those organizations in 2006 found that in 76 of the 80 US physics departments surveyed, a course using John David Jackson's Classical Electrodynamics was required for all first year graduate students. For undergraduates, there are several widely used textbooks, including David Griffiths' Introduction to Electrodynamics and Electricity and Magnetism by Edward Mills Purcell and D. J. Morin Also at an undergraduate level, Richard Feynman's classic The Feynman Lectures on Physics is available online to read for free.
 W
WMaxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon.
 W
WIn mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity.
 W
WIn thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
 W
WPoisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
 W
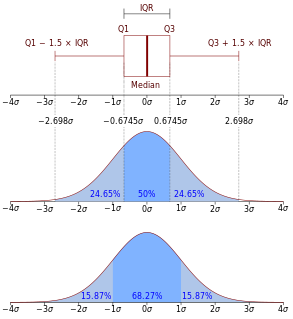
WIn probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.
 W
WIn physics, specifically relativistic quantum mechanics (RQM) and its applications to particle physics, relativistic wave equations predict the behavior of particles at high energies and velocities comparable to the speed of light. In the context of quantum field theory (QFT), the equations determine the dynamics of quantum fields. The solutions to the equations, universally denoted as ψ or Ψ, are referred to as "wave functions" in the context of RQM, and "fields" in the context of QFT. The equations themselves are called "wave equations" or "field equations", because they have the mathematical form of a wave equation or are generated from a Lagrangian density and the field-theoretic Euler–Lagrange equations.
 W
WThe second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. Entropy predicts the direction of spontaneous processes, and determines whether they are irreversible or impossible, despite obeying the requirement of conservation of energy, which is established in the first law of thermodynamics. The second law may be formulated by the observation that the entropy of isolated systems left to spontaneous evolution cannot decrease, as they always arrive at a state of thermodynamic equilibrium, where the entropy is highest. If all processes in the system are reversible, the entropy is constant.
 W
WIn quantum field theory, and in the significant subfields of quantum electrodynamics (QED) and quantum chromodynamics (QCD), the two-body Dirac equations (TBDE) of constraint dynamics provide a three-dimensional yet manifestly covariant reformulation of the Bethe–Salpeter equation for two spin-1/2 particles. Such a reformulation is necessary since without it, as shown by Nakanishi, the Bethe–Salpeter equation possesses negative-norm solutions arising from the presence of an essentially relativistic degree of freedom, the relative time. These "ghost" states have spoiled the naive interpretation of the Bethe–Salpeter equation as a quantum mechanical wave equation. The two-body Dirac equations of constraint dynamics rectify this flaw. The forms of these equations can not only be derived from quantum field theory they can also be derived purely in the context of Dirac's constraint dynamics and relativistic mechanics and quantum mechanics. Their structures, unlike the more familiar two-body Dirac equation of Breit, which is a single equation, are that of two simultaneous quantum relativistic wave equations. A single two-body Dirac equation similar to the Breit equation can be derived from the TBDE. Unlike the Breit equation, it is manifestly covariant and free from the types of singularities that prevent a strictly nonperturbative treatment of the Breit equation.
 W
WThe wave equation is an important second-order linear partial differential equation for the description of waves—as they occur in classical physics—such as mechanical waves or light waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics.
 W
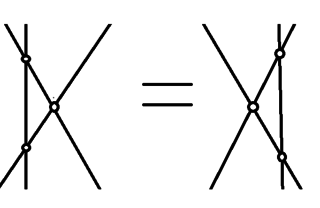
WIn physics, the Yang–Baxter equation is a consistency equation which was first introduced in the field of statistical mechanics. It depends on the idea that in some scattering situations, particles may preserve their momentum while changing their quantum internal states. It states that a matrix , acting on two out of three objects, satisfies