In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.
 W
WIn differential geometry, the associate family of a minimal surface is a one-parameter family of minimal surfaces which share the same Weierstrass data. That is, if the surface has the representation
 W
WIn differential geometry, the Björling problem is the problem of finding a minimal surface passing through a given curve with prescribed normal. The problem was posed and solved by Swedish mathematician Emanuel Gabriel Björling, with further refinement by Hermann Schwarz.
 W
WIn mathematics, Bour's minimal surface is a two-dimensional minimal surface, embedded with self-crossings into three-dimensional Euclidean space. It is named after Edmond Bour, whose work on minimal surfaces won him the 1861 mathematics prize of the French Academy of Sciences.
 W
WIn differential geometry, Catalan's minimal surface is a minimal surface originally studied by Eugène Charles Catalan in 1855.
 W
WA catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.
 W
WIn differential geometry, the Chen–Gackstatter surface family is a family of minimal surfaces that generalize the Enneper surface by adding handles, giving it nonzero topological genus.
 W
WIn mathematics, Costa's minimal surface, is an embedded minimal surface discovered in 1982 by the Brazilian mathematician Celso José da Costa. It is also a surface of finite topology, which means that it can be formed by puncturing a compact surface. Topologically, it is a thrice-punctured torus.
 W
WIn the mathematical theory of minimal surfaces, the double bubble conjecture states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble — three spherical surfaces meeting at angles of 2π/3 on a common circle. It is now a theorem, as a proof of it was published in 2002.
 W
WIn differential geometry and algebraic geometry, the Enneper surface is a self-intersecting surface that can be described parametrically by:
 W
WA gyroid is an infinitely connected triply periodic minimal surface discovered by Alan Schoen in 1970.
 W
WThe helicoid, after the plane and the catenoid, is the third minimal surface to be known.
 W
WIn differential geometry, the Henneberg surface is a non-orientable minimal surface named after Lebrecht Henneberg.
 W
WIn differential geometry, a k-noid is a minimal surface with k catenoid openings. In particular, the 3-noid is often called trinoid. The first k-noid minimal surfaces were described by Jorge and Meeks in 1983.
 W
WIn differential geometry, the lidinoid is a triply periodic minimal surface. The name comes from its Swedish discoverer Sven Lidin.
 W
WIn mathematics, a minimal surface of revolution or minimum surface of revolution is a surface of revolution defined from two points in a half-plane, whose boundary is the axis of revolution of the surface. It is generated by a curve that lies in the half-plane and connects the two points; among all the surfaces that can be generated in this way, it is the one that minimizes the surface area. A basic problem in the calculus of variations is finding the curve between two points that produces this minimal surface of revolution.
 W
WIn differential geometry, the Neovius surface is a triply periodic minimal surface originally discovered by Finnish mathematician Edvard Rudolf Neovius.
 W
WPlateau's laws describe the structure of soap films. These laws were formulated in the 19th century by the Belgian physicist Joseph Plateau from his experimental observations. Many patterns in nature are based on foams obeying these laws.
 W
WIn mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who experimented with soap films. The problem is considered part of the calculus of variations. The existence and regularity problems are part of geometric measure theory.
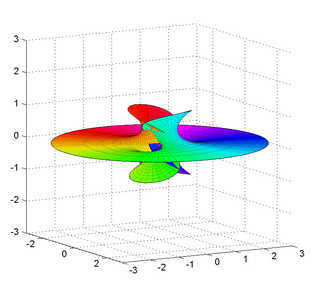 W
WIn differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.
 W
WIn differential geometry, Riemann's minimal surface is a one-parameter family of minimal surfaces described by Bernhard Riemann in a posthumous paper published in 1867. Surfaces in the family are singly periodic minimal surfaces with an infinite number of ends asymptotic to parallel planes, each plane "shelf" connected with catenoid-like bridges to the neighbouring ones. Their intersections with horizontal planes are circles or lines; Riemann proved that they were the only minimal surfaces fibered by circles in parallel planes besides the catenoid, helicoid and plane. They are also the only nontrivial embedded minimal surfaces in Euclidean 3-space invariant under the group generated by a nontrivial translation. It is possible to attach extra handles to the surfaces, producing higher-genus minimal surface families.
 W
WIn differential geometry, a saddle tower is a minimal surface family generalizing the singly periodic Scherk's second surface so that it has N-fold (N > 2) symmetry around one axis.
 W
WIn mathematics, a Scherk surface is an example of a minimal surface. Scherk described two complete embedded minimal surfaces in 1834; his first surface is a doubly periodic surface, his second surface is singly periodic. They were the third non-trivial examples of minimal surfaces. The two surfaces are conjugates of each other.
 W
WA soap bubble is an extremely thin film of soapy water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact with another object. They are often used for children's enjoyment, but they are also used in artistic performances. Assembling several bubbles results in foam.
 W
WIn differential geometry, a triply periodic minimal surface (TPMS) is a minimal surface in ℝ3 that is invariant under a rank-3 lattice of translations.
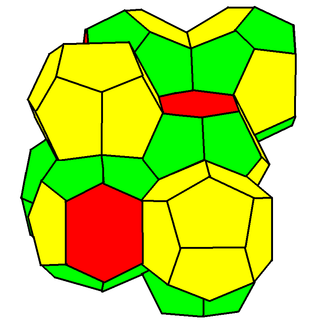 W
WIn geometry, the Weaire–Phelan structure is a complex 3-dimensional structure representing an idealised foam of equal-sized bubbles. In 1993, Trinity College Dublin physicist Denis Weaire and his student Robert Phelan found in computer simulations of foam that this structure was a better solution of the "Kelvin problem" than the previous best-known solution, the Kelvin structure.
 W
WIn mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.