28 Pyramids and bipyramids

A (symmetric) n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base. An n-gonal bipyramid has 2n triangle faces, 3n edges, and 2 + n vertices.

In geometry, a decagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If a decagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. It is an icosahedron, but not the regular one.

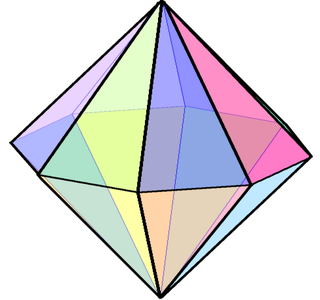
The heptagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an heptagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. The resulting solid has 14 triangular faces, 9 vertices and 21 edges.

The octagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an octagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. 16-sided dice are often octagonal bipyramids.

In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.

In geometry, the elongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid.

In geometry, the elongated hexagonal bipyramid is constructed by elongating a hexagonal bipyramid.

In geometry, the elongated pentagonal bipyramid or pentakis pentagonal prism is one of the Johnson solids (J16). As the name suggests, it can be constructed by elongating a pentagonal bipyramid (J13) by inserting a pentagonal prism between its congruent halves.

In geometry, the elongated pentagonal pyramid is one of the Johnson solids (J9). As the name suggests, it can be constructed by elongating a pentagonal pyramid (J2) by attaching a pentagonal prism to its base.

In geometry, the elongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal prism. Along with the set of pyramids, these figures are topologically self-dual.

In geometry, the elongated square bipyramid is one of the Johnson solids (J15). As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves.

In geometry, the elongated square pyramid is one of the Johnson solids (J8). As the name suggests, it can be constructed by elongating a square pyramid (J1) by attaching a cube to its square base. Like any elongated pyramid, it is topologically self-dual.

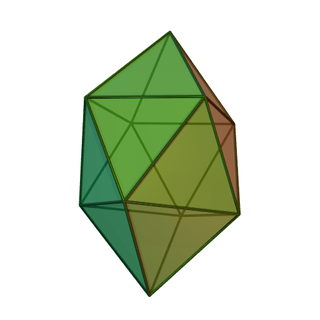
In geometry, the elongated triangular bipyramid or triakis triangular prism is one of the Johnson solids (J14), convex polyhedra whose faces are regular polygons. As the name suggests, it can be constructed by elongating a triangular bipyramid (J12) by inserting a triangular prism between its congruent halves.

In geometry, the elongated triangular pyramid is one of the Johnson solids (J7). As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically self-dual.

In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.

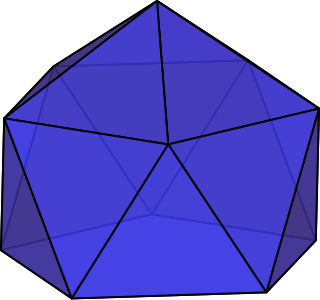
In geometry, the gyroelongated pentagonal pyramid is one of the Johnson solids (J11). As its name suggests, it is formed by taking a pentagonal pyramid and "gyroelongating" it, which in this case involves joining a pentagonal antiprism to its base.

In geometry, the gyroelongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal antiprism.

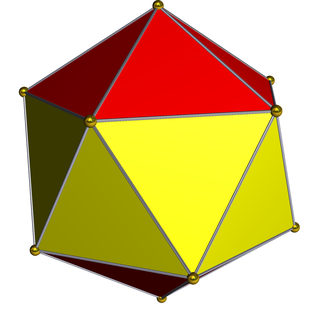
In geometry, the gyroelongated square bipyramid, heccaidecadeltahedron, or tetrakis square antiprism is one of the Johnson solids (J17). As the name suggests, it can be constructed by gyroelongating an octahedron by inserting a square antiprism between its congruent halves. It is one of the eight strictly-convex deltahedra.

In geometry, the gyroelongated square pyramid is one of the Johnson solids (J10). As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base.

A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point. Like any pyramid, it is self-dual.

In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids. Each bipyramid is the dual of a uniform prism.

In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point. Like any pyramid, it is self-dual.

In geometry, the pentagrammic bipyramid is first of the infinite set of face-transitive star bipyramids containing star polygon arrangement of edges. It has 10 intersecting isosceles triangle faces. It is topologically identical to the pentagonal bipyramid.

In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has C4v symmetry. If all edges are equal, it is an equilateral square pyramid, the Johnson solid J1.

In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces.

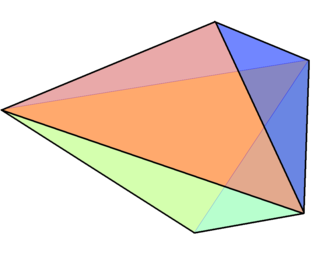
In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.