 W
WIn recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The order of the magic square is the number of integers along one side (n), and the constant sum is called the magic constant. If the array includes just the positive integers , the magic square is said to be normal. Some authors take magic square to mean normal magic square.
 W
WAhmad ibn ‘Ali al-Buni, also called Sharaf al-Din or Shihab al-Din Ahmad ibn Ali ibn Yusuf al-Buni al-Maliki al-ifriqi was an Arab mathematician and philosopher and a well known Sufi and writer on the esoteric value of letters and topics relating to mathematics, sihr (sorcery) and spirituality, but very little is known about him. Al-Buni lived in Egypt and learned from many eminent Sufi masters of his time.
 W
WAn associative magic square is a magic square for which each pair of numbers symmetrically opposite to the center sum up to the same value. For an square, filled with the numbers from to , this common sum must equal . These squares are also called associated magic squares, regular magic squares, regmagic squares, or symmetric magic squares.
 W
WClaude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse, at that time belonging to Duchy of Savoy.
 W
WWalter William Rouse Ball, known as W. W. Rouse Ball, was a British mathematician, lawyer, and fellow at Trinity College, Cambridge, from 1878 to 1905. He was also a keen amateur magician, and the founding president of the Cambridge Pentacle Club in 1919, one of the world's oldest magic societies.
 W
WArthur Cayley was a prolific British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics.
 W
WBernard Frénicle de Bessy, was a French mathematician born in Paris, who wrote numerous mathematical papers, mainly in number theory and combinatorics. He is best remembered for Des quarrez ou tables magiques, a treatise on magic squares published posthumously in 1693, in which he described all 880 essentially different normal magic squares of order 4. The Frénicle standard form, a standard representation of magic squares, is named after him. He solved many problems created by Fermat and also discovered the cube property of the number 1729, later referred to as a taxicab number. He is also remembered for his treatise Traité des triangles rectangles en nombres published in 1676.
 W
WA geometric magic square, often abbreviated to geomagic square, is a generalization of magic squares invented by Lee Sallows in 2001. A traditional magic square is a square array of numbers whose sum taken in any row, any column, or in either diagonal is the same target number. A geomagic square, on the other hand, is a square array of geometrical shapes in which those appearing in each row, column, or diagonal can be fitted together to create an identical shape called the target shape. As with numerical types, it is required that the entries in a geomagic square be distinct. Similarly, the eight trivial variants of any square resulting from its rotation and/or reflection, are all counted as the same square. By the dimension of a geomagic square is meant the dimension of the pieces it uses. Hitherto interest has focused mainly on 2D squares using planar pieces, but pieces of any dimension are permitted.
 W
WDattatreya Ramchandra Kaprekar (1905–1986) was an Indian recreational mathematician who described several classes of natural numbers including the Kaprekar, harshad and self numbers and discovered the Kaprekar's constant, named after him. Despite having no formal postgraduate training and working as a schoolteacher, he published extensively and became well known in recreational mathematics circles.
 W
WPhilippe de La Hire was a French painter, mathematician, astronomer, and architect. According to Bernard le Bovier de Fontenelle he was an "academy unto himself".
 W
WSimon de la Loubère was a French diplomat to Siam (Thailand), writer, mathematician and poet. He is credited with bringing back a document which introduced Europe to Indian astronomy, the "Siamese method" of making magic squares, as well as one of the earliest description of parachutes.
 W
WLo Shu Square, or the Nine Halls Diagram, is the unique normal magic square of order three. The Lo Shu is part of the legacy of ancient Chinese mathematical and divinatory traditions, and is an important emblem in Feng Shui (風水), the art of geomancy concerned with the placement of objects in relation to the flow of qi (氣) "natural energy".
 W
WThe magic constant or magic sum of a magic square is the sum of numbers in any row, column, or diagonal of the magic square. For example, the magic square shown below has a magic constant of 15. In general where is the side length of the square.
 W
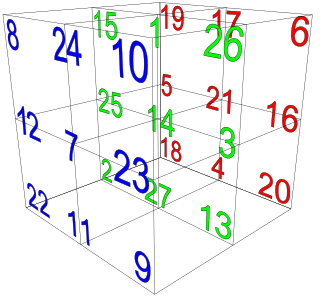
WIn mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal to the same number, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant
 W
WA magic hexagon of order n is an arrangement of numbers in a centered hexagonal pattern with n cells on each edge, in such a way that the numbers in each row, in all three directions, sum to the same magic constant M. A normal magic hexagon contains the consecutive integers from 1 to 3n2 − 3n + 1. It turns out that normal magic hexagons exist only for n = 1 and n = 3. Moreover, the solution of order 3 is essentially unique. Meng also gave a less intricate constructive proof.
 W
WA magic hexagram of order 2 is an arrangement of numbers in a hexagram with triangular cell with 2 cells on each edge, in such a way that the numbers in each row, in all three directions, sum to the same magic constant M.
 W
WAn n-pointed magic star is a star polygon with Schläfli symbol {n/2} in which numbers are placed at each of the n vertices and n intersections, such that the four numbers on each line sum to the same magic constant. A normal magic star contains the consecutive integers 1 to 2n. No numbers are ever repeated. The magic constant of an n-pointed normal magic star is M = 4n + 2.
 W
WA most-perfect magic square of doubly even order n = 4k is a pan-diagonal magic square containing the numbers 1 to n2 with three additional properties:Each 2×2 subsquare, including wrap-round, sums to s/k, where s = n(n2 + 1)/2 is the magic sum. All pairs of integers distant n/2 along any diagonal are complementary.
 W
WThe square array of the integers 1 through n2 that is generated when a method for constructing a 4 × 4 magic square is generalized was called a mystic square by Joel B. Wolowelsky and David Shakow in their article describing a method for constructing a magic square whose order is a multiple of 4. A 4 × 4 magic square can be constructed by writing out the numbers from 1 to 16 consecutively in a 4 × 4 matrix and then interchanging those numbers on the diagonals that are equidistant from the center.. The sum of each row, column and diagonal is 34, the “magic number” for a 4 × 4 magic square. In general, the “magic number” for an n × n magic square is n(n^2 + 1)/2.
 W
WFra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and an early contributor to the field now known as accounting. He is referred to as "The Father of Accounting and Bookkeeping" in Europe and he was the second person to publish a work on the double-entry system of book-keeping on the continent. He was also called Luca di Borgo after his birthplace, Borgo Sansepolcro, Tuscany.
 W
WLee Cecil Fletcher Sallows is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares.
 W
WRichard C. Schroeppel is an American mathematician born in Illinois. His research has included magic squares, elliptic curves, and cryptography. In 1964, Schroeppel won first place in the United States among over 225,000 high school students in the Annual High School Mathematics Examination, a contest sponsored by the Mathematical Association of America and the Society of Actuaries. In both 1966 and 1967, Schroeppel scored among the top 5 in the U.S. in the William Lowell Putnam Mathematical Competition. In 1973 he discovered that there are 275,305,224 normal magic squares of order 5. In 1998–1999 he designed the Hasty Pudding Cipher which was a candidate for the Advanced Encryption Standard, and he is one of the designers of the SANDstorm hash, a submission to the NIST SHA-3 competition.
 W
WThe Siamese method, or De la Loubère method, is a simple method to construct any size of n-odd magic squares. The method was brought to France in 1688 by the French mathematician and diplomat Simon de la Loubère, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic squares straightforward.
 W
WA simple magic cube is the lowest of six basic classes of magic cube. These classes are based on extra features required.
 W
WIn geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
 W
WSriramachakra is a mystic diagram or a yantra given in Tamil almanacs as an instrument of astrology for predicting one's future. The geometrical diagram consists of a square divided into smaller squares by equal numbers of lines parallel to the sides of the square. Certain integers in well defined patterns are written in the various smaller squares. In some almanacs, for example, in the Panchangam published by the Sringeri Sharada Peetham or the Pnachangam published by Srirangam Temple, the diagram takes the form of a magic square of order 4 with certain special properties. This magic square belongs to a certain class of magic squares called strongly magic squares which has been so named and studied by T V Padmakumar, an amateur mathematician from Thiruvananthapuram, Kerala. In some almanacs, for example, in the Pambu Panchangam, the diagram consists of an arrangement of 36 small squares in 6 rows and 6 columns in which the digits 1, 2, ..., 9 are written in that order from left to right starting from the top-left corner, repeating the digits in the same direction once the digit 9 is reached.
 W
WWater retention on mathematical surfaces is the catching of water in ponds on a surface of cells of various heights on a regular array such as a square lattice, where water is rained down on every cell in the system. The boundaries of the system are open and allow water to flow out. Water will be trapped in ponds, and eventually all ponds will fill to their maximum height, with any additional water flowing over spillways and out the boundaries of the system. The problem is to find the amount of water trapped or retained for a given surface. This has been studied extensively for two mathematical surfaces: magic squares and random surfaces. The model can also be applied to the triangular grid.
 W
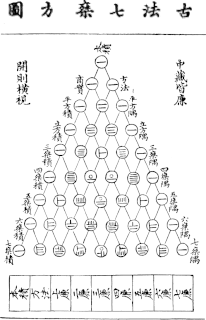
WYang Hui, courtesy name Qianguang (謙光), was a Chinese mathematician and writer during the Song dynasty. Originally, from Qiantang, Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting Yang Hui's Triangle. This triangle was the same as Pascal's Triangle, discovered by Yang's predecessor Jia Xian. Yang was also a contemporary to the other famous mathematician Qin Jiushao.
 W
WThe Yellow River Map, Scheme, or Diagram is an ancient Chinese concept. It is related to the Lo Shu Square. The origins of the two from the rivers Luo and He are part of Chinese mythology. The development of the two are part of Chinese philosophy. (Wu:52)