31 6 polytopes

In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.

In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 (for its 72 vertices).

In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure. It is also called the Schläfli polytope.

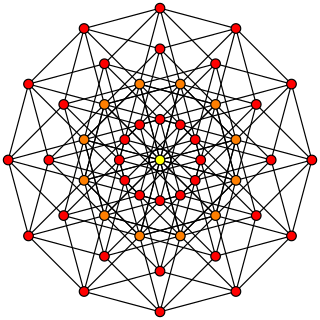
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.

In geometry, a 6-demicube or demihexteract is a uniform 6-polytope, constructed from a 6-cube (hexeract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

In geometry, a 6-orthoplex, or 6-cross polytope, is a regular 6-polytope with 12 vertices, 60 edges, 160 triangle faces, 240 tetrahedron cells, 192 5-cell 4-faces, and 64 5-faces.

In 6-dimensional geometry, there are 35 uniform polytopes with A6 symmetry. There is one self-dual regular form, the 6-simplex with 7 vertices.

In 6-dimensional geometry, there are 64 uniform polytopes with B6 symmetry. There are two regular forms, the 6-orthoplex, and 6-cube with 12 and 64 vertices respectively. The 6-demicube is added with half the symmetry.

In six-dimensional geometry, a cantellated 6-cube is a convex uniform 6-polytope, being a cantellation of the regular 6-cube.

In six-dimensional geometry, a cantellated 6-orthoplex is a convex uniform 6-polytope, being a cantellation of the regular 6-orthoplex.

In six-dimensional geometry, a cantellated 6-simplex is a convex uniform 6-polytope, being a cantellation of the regular 6-simplex.

In six-dimensional geometry, a cantic 6-cube is a uniform 6-polytope.

In five-dimensional Euclidean geometry, the cyclotruncated 5-simplex honeycomb or cyclotruncated hexateric honeycomb is a space-filling tessellation. It is composed of 5-simplex, truncated 5-simplex, and bitruncated 5-simplex facets in a ratio of 1:1:1.

In 6-dimensional geometry, there are 47 uniform polytopes with D6 symmetry, 16 are unique, and 31 are shared with the B6 symmetry. There are two regular forms, the 6-orthoplex, and 6-demicube with 12 and 32 vertices respectively.

In 6-dimensional geometry, there are 39 uniform polytopes with E6 symmetry. The two simplest forms are the 221 and 122 polytopes, composed of 27 and 72 vertices respectively.

In six-dimensional geometry, a pentellated 6-cube is a convex uniform 6-polytope with 5th order truncations of the regular 6-cube.

In six-dimensional geometry, a pentellated 6-orthoplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-orthoplex.

In six-dimensional geometry, a pentellated 6-simplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-simplex.

In six-dimensional geometry, a pentic 6-cube is a convex uniform 6-polytope.

In six-dimensional geometry, a rectified 6-cube is a convex uniform 6-polytope, being a rectification of the regular 6-cube.

In six-dimensional geometry, a rectified 6-orthoplex is a convex uniform 6-polytope, being a rectification of the regular 6-orthoplex.

In six-dimensional geometry, a rectified 6-simplex is a convex uniform 6-polytope, being a rectification of the regular 6-simplex.

In six-dimensional geometry, a runcic 6-cube is a convex uniform 6-polytope. There are 2 unique runcic for the 6-cube.

In six-dimensional geometry, a runcinated 6-orthplex is a convex uniform 6-polytope with 3rd order truncations (runcination) of the regular 6-orthoplex.

In six-dimensional geometry, a runcinated 6-simplex is a convex uniform 6-polytope constructed as a runcination of the regular 6-simplex.

In six-dimensional geometry, a steric 6-cube is a convex uniform 6-polytope. There are unique 4 steric forms of the 6-cube.

In six-dimensional geometry, a stericated 6-cube is a convex uniform 6-polytope, constructed as a sterication of the regular 6-cube.

In six-dimensional geometry, a stericated 6-orthoplex is a convex uniform 6-polytope, constructed as a sterication of the regular 6-orthoplex.

In six-dimensional geometry, a stericated 6-simplex is a convex uniform 6-polytope with 4th order truncations (sterication) of the regular 6-simplex.

In six-dimensional geometry, a truncated 6-simplex is a convex uniform 6-polytope, being a truncation of the regular 6-simplex.

In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.