 W
WElementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels.
 W
WIn common usage, the abscissa refers to the horizontal (x) axis and the ordinate refers to the vertical (y) axis of a standard two-dimensional graph.
 W
WIn mathematics, the arguments of the maxima are the points, or elements, of the domain of some function at which the function values are maximized. In contrast to global maxima, which refers to the largest outputs of a function, arg max refers to the inputs, or arguments, at which the function outputs are as large as possible.
 W
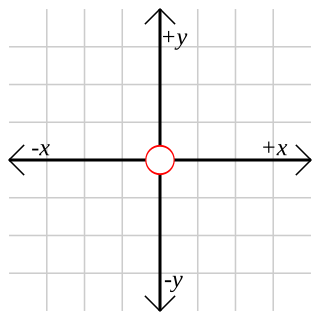
WA Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.
 W
WIn combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation. A circular shift is a special kind of cyclic permutation, which in turn is a special kind of permutation. Formally, a circular shift is a permutation σ of the n entries in the tuple such that either modulo n, for all entries i = 1, ..., n
 W
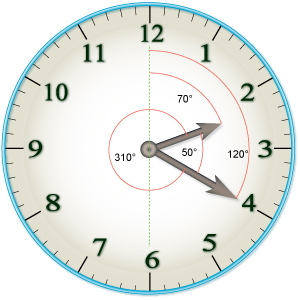
WClock angle problems are a type of mathematical problem which involve finding the angle between the hands of an analog clock.
 W
WIn mathematics, a constant function is a function whose (output) value is the same for every input value. For example, the function y(x) = 4 is a constant function because the value of y(x) is 4 regardless of the input value x.
 W
WCyrillic numerals are a numeral system derived from the Cyrillic script, developed in the First Bulgarian Empire in the late 10th century. It was used in the First Bulgarian Empire and by South and East Slavic peoples. The system was used in Russia as late as the early 18th century, when Peter the Great replaced it with Arabic numerals as part of his civil script reform initiative. Cyrillic numbers played a role in Peter the Great's currency reform plans, too, with silver wire kopecks issued after 1696 and mechanically minted coins issued between 1700 and 1722 inscribed with the date using Cyrillic numerals. By 1725, Russian Imperial coins had transitioned to Arabic numerals. The Cyrillic numerals may still be found in books written in the Church Slavonic language.
 W
WIn mathematics, a function is a binary relation between two sets that associates every element of the first set to exactly one element of the second set. Typical examples are functions from integers to integers, or from the real numbers to real numbers.
 W
WGlagolitic numerals are a numeral system derived from the Glagolitic script, generally agreed to have been created in the 9th century by Saint Cyril. They are similar to Cyrillic numerals, except that numeric values are assigned according to the native alphabetic order of the Glagolitic alphabet. Use of Glagolitic script and numerals declined through the Middle Ages and by the 17th century Glagolitic was used almost only in religious writings. It is unclear if the use of Glagolitic numerals persisted as long as the use of Glagolitic script.
 W
WThe Hindu–Arabic numeral system or Indo-Arabic numeral system is a positional decimal numeral system, and is the most common system for the symbolic representation of numbers in the world.
 W
WHooper's paradox is a falsidical paradox based on a optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units.
 W
WIn mathematics, an identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument. That is, for f being identity, the equality f(x) = x holds for all x.
 W
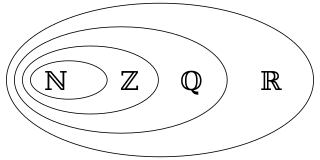
WAn integer is colloquially defined as a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 5+1/2, and √2 are not.
 W
WMathematical beauty is the aesthetic pleasure typically derived from the abstractness, purity, simplicity, depth or orderliness of mathematics. Mathematicians often express this pleasure by describing mathematics as beautiful. They might also describe mathematics as an art form or, at a minimum, as a creative activity. Comparisons are often made with music and poetry.
 W
WThe missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it.
 W
WIn mathematics, the natural numbers are those used for counting and ordering. In common mathematical terminology, words colloquially used for counting are "cardinal numbers", and words used for ordering are "ordinal numbers". The natural numbers can, at times, appear as a convenient set of codes ; that is, as what linguists call nominal numbers, forgoing many or all of the properties of being a number in a mathematical sense. The set of natural numbers is often denoted by the symbol .
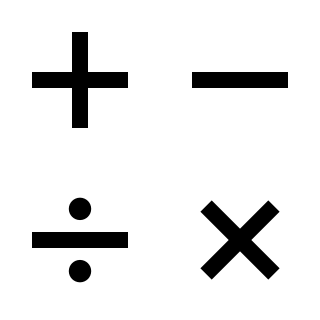 W
WIn mathematics, an operation is a function which takes zero or more input values to a well-defined output value. The number of operands is the arity of the operation.
 W
WIn mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space.
 W
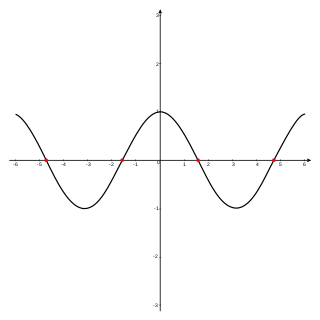
WA periodic function is a function that repeats its values at regular intervals, for example, the trigonometric functions, which repeat at intervals of 2π radians. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic.
 W
WIn mathematics, a ratio indicates how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six. Similarly, the ratio of lemons to oranges is 6∶8 and the ratio of oranges to the total amount of fruit is 8∶14.
 W
WIn mathematics, a rational number is a number such as -3/7 that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Every integer is a rational number: for example, 5 = 5/1. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
 W
WIn mathematics, a real number is a value of a continuous quantity that can represent a distance along a line. The adjective real in this context was introduced in the 17th century by René Descartes, who distinguished between real and imaginary roots of polynomials. The real numbers include all the rational numbers, such as the integer −5 and the fraction 4/3, and all the irrational numbers, such as √2. Included within the irrationals are the transcendental numbers, such as π (3.14159265...). In addition to measuring distance, real numbers can be used to measure quantities such as time, mass, energy, velocity, and many more. The set of real numbers is denoted using the symbol R or .
 W
WIn mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function whose domain is either the set of the natural numbers, or the set of the first n natural numbers.
 W
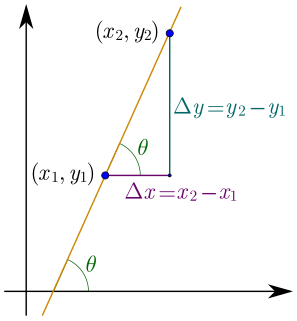
WIn mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but its earliest use in English appears in O'Brien (1844) who wrote the equation of a straight line as "y = mx + b" and it can also be found in Todhunter (1888) who wrote it as "y = mx + c".
 W
WIn mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16. Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by where the symbol is called the radical sign or radix. For example, the principal square root of 9 is 3, which is denoted by because 32 = 3 ⋅ 3 = 9 and 3 is nonnegative. The term (or number) whose square root is being considered is known as the radicand. The radicand is the number or expression underneath the radical sign, in this case 9.
 W
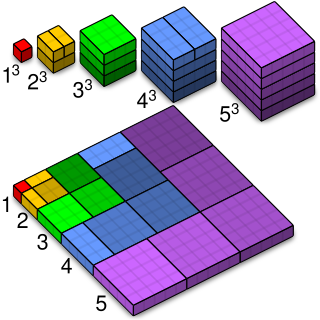
WIn number theory, the sum of the first n cubes is the square of the nth triangular number. That is,
 W
WTally marks, also called hash marks, are a unary numeral system. They are a form of numeral used for counting. They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no intermediate results need to be erased or discarded.
 W
WIn mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .
 W
WIn analytic geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. As such, these points satisfy x = 0.
 W
WIn mathematics, a zero of a real-, complex-, or generally vector-valued function , is a member of the domain of such that vanishes at ; that is, the function attains the value of 0 at , or equivalently, is the solution to the equation . A "zero" of a function is thus an input value that produces an output of .