33 Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.

In mathematics, a 3-sphere, or glome, is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

The Alexander horned sphere is a pathological object in topology discovered by J. W. Alexander (1924).

In mathematics, the Borromean rings consist of three topological circles which are linked but where removing any one ring leaves the other two unconnected. In other words, no two of the three rings are linked with each other as a Hopf link, but nonetheless all three are linked. The Borromean rings are one of a class of such links called Brunnian links.

In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901. He discovered it on assignment from David Hilbert to prove that the projective plane could not be immersed in 3-space.

In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the cartesian product of two circles S1a and S1b. It is named after William Kingdon Clifford. It resides in R4, as opposed to in R3. To see why R4 is necessary, note that if S1a and S1b each exists in its own independent embedding space R2a and R2b, the resulting product space will be R4 rather than R3. The historically popular view that the cartesian product of two circles is an R3 torus in contrast requires the highly asymmetric application of a rotation operator to the second circle, since that circle will only have one independent axis z available to it after the first circle consumes x and y.

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.

The Dimensionally Extended 9-Intersection Model (DE-9IM) is a topological model and a standard used to describe the spatial relations of two regions, in geometry, point-set topology, geospatial topology, and fields related to computer spatial analysis. The spatial relations expressed by the model are invariant to rotation, translation and scaling transformations.

In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.

In geometric topology, the dogbone space, constructed by R. H. Bing (1957), is a quotient space of three-dimensional Euclidean space such that all inverse images of points are points or tame arcs, yet it is not homeomorphic to . The name "dogbone space" refers to a fanciful resemblance between some of the diagrams of genus 2 surfaces in R. H. Bing's paper and a dog bone. Bing (1959) showed that the product of the dogbone space with is homeomorphic to .

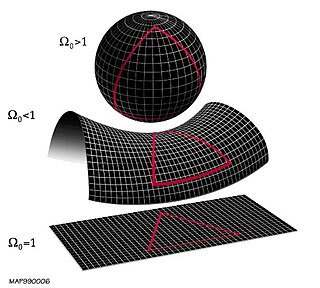
In mathematics, genus has a few different, but closely related, meanings. The most common concept, the genus of an (orientable) surface, is the number of "holes" it has, so that a sphere has genus 0 and a torus has genus 1. This is made more precise below.

In geometry, an Hadamard space, named after Jacques Hadamard, is a non-linear generalization of a Hilbert space. In the literature they are also equivalently defined as complete CAT(0) spaces.

In mathematics, a handle decomposition of an m-manifold M is a union

In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds. Handles are used to particularly study 3-manifolds.

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.

In mathematics, an I-bundle is a fiber bundle whose fiber is an interval and whose base is a manifold. Any kind of interval, open, closed, semi-open, semi-closed, open-bounded, compact, even rays, can be the fiber.

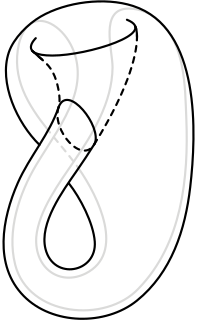
In topology, a branch of mathematics, the Klein bottle is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined. Informally, it is a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary.

In geometric topology, a branch of mathematics, the lantern relation is a relation that appears between certain Dehn twists in the mapping class group of a surface. The most general version of the relation involves seven Dehn twists. The relation was discovered by Dennis Johnson in 1979.

In topography, the line of greatest slope is a curve following the steepest slope. In mountain biking and skiing, the line of greatest slope is sometimes called the fall line.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

In topology, a branch of mathematics, Pachner moves, named after Udo Pachner, are ways of replacing a triangulation of a piecewise linear manifold by a different triangulation of a homeomorphic manifold. Pachner moves are also called bistellar flips. Any two triangulations of a piecewise linear manifold are related by a finite sequence of Pachner moves.

In geometric topology, PDIFF, for piecewise differentiable, is the category of piecewise-smooth manifolds and piecewise-smooth maps between them. It properly contains DIFF and PL, and the reason it is defined is to allow one to relate these two categories. Further, piecewise functions such as splines and polygonal chains are common in mathematics, and PDIFF provides a category for discussing them.

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin.

In physical knot theory, each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot. Knots and links that minimize ropelength are called ideal knots and ideal links respectively.

In topology and in calculus, a round function is a scalar function , over a manifold , whose critical points form one or several connected components, each homeomorphic to the circle , also called critical loops. They are special cases of Morse-Bott functions.

In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h: K → X.

In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.

In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm; that is, whether the problem lies in the complexity class P.

In knot theory, the Whitehead link, named for J. H. C. Whitehead, is one of the most basic links.

In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to . J. H. C. Whitehead (1935) discovered this puzzling object while he was trying to prove the Poincaré conjecture, correcting an error in an earlier paper Whitehead where he incorrectly claimed that no such manifold exists.