35 Algebraic topology

Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.

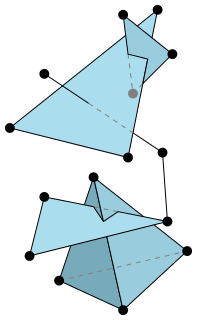
House with two rooms or Bing's house is a particular contractible, 2-dimensional simplicial complex that is not collapsible. The name was given by R. H. Bing.

In mathematics, a 3-sphere, or glome, is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

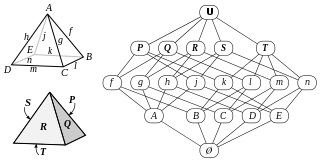
In mathematics, an abstract polytope is an algebraic partially ordered set or poset which captures the combinatorial properties of a traditional polytope without specifying purely geometric properties such as angles or edge lengths. A polytope is a generalisation of polygons and polyhedra into any number of dimensions.

In combinatorics, an abstract simplicial complex (ASC) is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

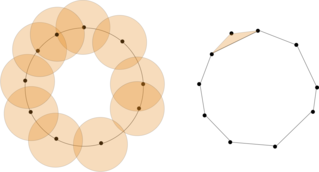
In algebraic topology and topological data analysis, the Čech complex is an abstract simplicial complex constructed from a point cloud in any metric space which is meant to capture topological information about the point cloud or the distribution it is drawn from. Given a finite point cloud X and an ε > 0, we construct the Čech complex as follows: Take the elements of X as the vertex set of . Then, for each , let if the set of ε-balls centered at points of σ has a nonempty intersection. In other words, the Čech complex is the nerve of the set of ε-balls centered at points of X. By the nerve lemma, the Čech complex is homotopy equivalent to the union of the balls.

Clique complexes, flag complexes, and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.

In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds of the same dimension are cobordant if their disjoint union is the boundary of a compact manifold one dimension higher.

In topology, especially algebraic topology, the cone of a topological space is the quotient space:

In mathematics, a configuration space is a construction closely related to state spaces or phase spaces in physics. In physics, these are used to describe the state of a whole system as a single point in a high-dimensional space. In mathematics, they are used to describe assignments of a collection of points to positions in a topological space. More specifically, configuration spaces in mathematics are particular examples of configuration spaces in physics in the particular case of several non-colliding particles.

In mathematics, specifically algebraic topology, a covering map is a continuous function from a topological space to a topological space such that each point in has an open neighbourhood evenly covered by . In this case, is called a covering space and the base space of the covering projection. The definition implies that every covering map is a local homeomorphism.

In mathematics, a cubical complex or cubical set is a set composed of points, line segments, squares, cubes, and their n-dimensional counterparts. They are used analogously to simplicial complexes and CW complexes in the computation of the homology of topological spaces.

In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.

In topology, the dunce hat is a compact topological space formed by taking a solid triangle and gluing all three sides together, with the orientation of one side reversed. Simply gluing two sides oriented in the same direction would yield a cone much like the dunce cap, but the gluing of the third side results in identifying the base of the cap with a line joining the base to the point.

The duocylinder, or double cylinder, is a geometric object embedded in 4-dimensional Euclidean space, defined as the Cartesian product of two disks of respective radii r1 and r2:

In mathematics, genus has a few different, but closely related, meanings. The most common concept, the genus of an (orientable) surface, is the number of "holes" it has, so that a sphere has genus 0 and a torus has genus 1. This is made more precise below.

In mathematics, an open cover of a topological space is a family of open subsets such that is the union of all of the open sets. A good cover is an open cover in which all sets and all intersections of finitely-many sets are contractible.

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.

In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by or , is defined to be the quotient space

In mathematics, especially homotopy theory, the mapping cone is a construction of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated . Its dual, a fibration, is called the mapping fibre. The mapping cone can be understood to be a mapping cylinder , with one end of the cylinder collapsed to a point. Thus, mapping cones are frequently applied in the homotopy theory of pointed spaces.

In algebraic topology, the Massey product is a cohomology operation of higher order introduced in, which generalizes the cup product. The Massey product was created by William S. Massey, an American algebraic topologist.

In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they "run round" a singularity. As the name implies, the fundamental meaning of monodromy comes from "running round singly". It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we "run round" a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what does happen as we "run round" in one dimension. Lack of monodromy is sometimes called polydromy.

In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n. In other words, given an inductive definition of a complex, the n-skeleton is obtained by stopping at the n-th step.

In geometry, ramification is 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign. The term is also used from the opposite perspective as when a covering map degenerates at a point of a space, with some collapsing of the fibers of the mapping.

In mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.

In the mathematical field of topology, a section of a fiber bundle is a continuous right inverse of the projection function . In other words, if is a fiber bundle over a base space, :

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.

In mathematics, a solenoid is a compact connected topological space that may be obtained as the inverse limit of an inverse system of topological groups and continuous homomorphisms(Si, fi), fi: Si+1 → Si, i ≥ 0,

In geometry, the tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.

In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h: K → X.

In topology, the Vietoris–Rips complex, also called the Vietoris complex or Rips complex, is an abstract simplicial complex that can be defined from any metric space M and distance δ by forming a simplex for every finite set of points that has diameter at most δ. That is, it is a family of finite subsets of M, in which we think of a subset of k points as forming a (k − 1)-dimensional simplex ; if a finite set S has the property that the distance between every pair of points in S is at most δ, then we include S as a simplex in the complex.

In knot theory, the Whitehead link, named for J. H. C. Whitehead, is one of the most basic links.

In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point. The winding number depends on the orientation of the curve, and is negative if the curve travels around the point clockwise.