36 Mathematical games

A mathematical game is a game whose rules, strategies, and outcomes are defined by clear mathematical parameters. Often, such games have simple rules and match procedures, such as Tic-tac-toe and Dots and Boxes. Generally, mathematical games need not be conceptually intricate to involve deeper computational underpinnings. For example, even though the rules of Mancala are relatively basic, the game can be rigorously analyzed through the lens of combinatorial game theory.

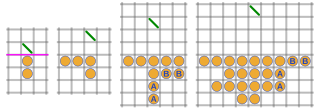
Chomp is a two-player strategy game played on a rectangular grid made up of smaller square cells, which can be thought of as the blocks of a chocolate bar. The players take it in turns to choose one block and "eat it", together with those that are below it and to its right. The top left block is "poisoned" and the player who eats this loses.

Conway's Soldiers or the checker-jumping problem is a one-person mathematical game or puzzle devised and analyzed by mathematician John Horton Conway in 1961. A variant of peg solitaire, it takes place on an infinite checkerboard. The board is divided by a horizontal line that extends indefinitely. Above the line are empty cells and below the line are an arbitrary number of game pieces, or "soldiers". As in peg solitaire, a move consists of one soldier jumping over an adjacent soldier into an empty cell, vertically or horizontally, and removing the soldier which was jumped over. The goal of the puzzle is to place a soldier as far above the horizontal line as possible.

Cram is a mathematical game played on a sheet of graph paper. It is the impartial version of Domineering and the only difference in the rules is that each player may place their dominoes in either orientation, but it results in a very different game. It has been called by many names, including "plugg" by Geoffrey Mott-Smith, and "dots-and-pairs." Cram was popularized by Martin Gardner in Scientific American.

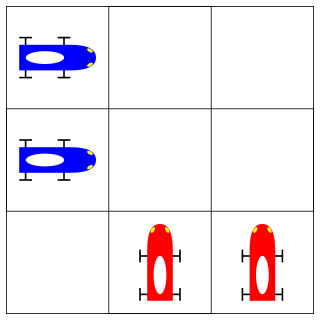
Dodgem is a simple abstract strategy game invented by Colin Vout in 1972 while he was a mathematics student at the University of Cambridge as described in the book Winning Ways. It is played on an n×n board with n-1 cars for each player—two cars each on a 3×3 board is enough for an interesting game, but larger sizes are also possible.

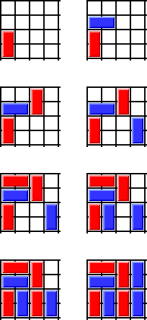
Domineering is a mathematical game that can be played on any collection of squares on a sheet of graph paper. For example, it can be played on a 6×6 square, a rectangle, an entirely irregular polyomino, or a combination of any number of such components. Two players have a collection of dominoes which they place on the grid in turn, covering up squares. One player places tiles vertically, while the other places them horizontally. As in most games in combinatorial game theory, the first player who cannot move loses.

Dots is an abstract strategy game, played by two or more people on a sheet of squared paper. The game is superficially similar to Go, in that the goal is to "capture" enemy dots by surrounding them with a continuous line of one's own dots. Once an area containing enemy dots is surrounded, that area ceases to be playable.

Dots and Boxes is a pencil-and-paper game for two players. It was first published in the 19th century by French mathematician Édouard Lucas, who called it la pipopipette. It has gone by many other names, including the game of dots, dot to dot grid, boxes, and pigs in a pen.

Fibonacci nim is a mathematical subtraction game, a variant of the game of nim. The game was first described by Michael J. Whinihan in 1963, who credits its invention to Robert E. Gaskell. It is called Fibonacci nim because the Fibonacci numbers feature heavily in its analysis.

In combinatorial game theory, a two-player deterministic perfect information turn-based game is a first-player-win if with perfect play the first player to move can always force a win. Similarly, a game is second-player-win if with perfect play the second player to move can always force a win. With perfect play, if neither side can force a win, the game is a draw.

Ghost Leg, known in Japan as Amidakuji or in Korea as Sadaritagi, is a method of lottery designed to create random pairings between two sets of any number of things, as long as the number of elements in each set is the same. This is often used to distribute things among people, where the number of things distributed is the same as the number of people. For instance, chores or prizes could be assigned fairly and randomly this way.

Grundy's game is a two-player mathematical game of strategy. The starting configuration is a single heap of objects, and the two players take turn splitting a single heap into two heaps of different sizes. The game ends when only heaps of size two and smaller remain, none of which can be split unequally. The game is usually played as a normal play game, which means that the last person who can make an allowed move wins.

Hackenbush is a two-player game invented by mathematician John Horton Conway. It may be played on any configuration of colored line segments connected to one another by their endpoints and to a "ground" line.

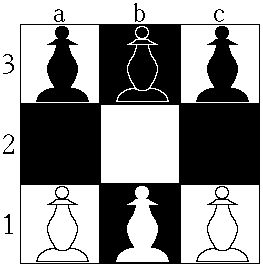
Hexapawn is a deterministic two-player game invented by Martin Gardner. It is played on a rectangular board of variable size, for example on a 3×3 board or on a chessboard. On a board of size n×m, each player begins with m pawns, one for each square in the row closest to them. The goal of each player is to advance one of their pawns to the opposite end of the board or to prevent the other player from moving.

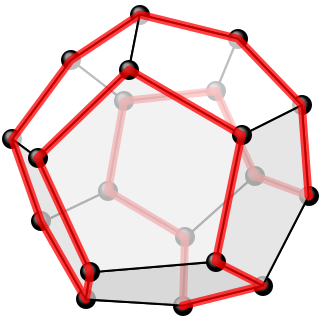
The icosian game is a mathematical game invented in 1857 by William Rowan Hamilton. The game's object is finding a Hamiltonian cycle along the edges of a dodecahedron such that every vertex is visited a single time, and the ending point is the same as the starting point. The puzzle was distributed commercially as a pegboard with holes at the nodes of the dodecahedral graph and was subsequently marketed in Europe in many forms.

The Integration Bee is an annual integral calculus competition pioneered in 1981 by the Massachusetts Institute of Technology. Similar contests are now regularly conducted in major United States universities, including Florida Polytechnic University, the State University of New York, the University of Florida, and elsewhere.

Kayles is a simple impartial game in combinatorial game theory, invented by Henry Dudeney in 1908. Given a row of imagined bowling pins, players take turns to knock out either one pin, or two adjacent pins, until all the pins are gone. Using the notation of octal games, Kayles is denoted 0.77.

The L game is a simple abstract strategy board game invented by Edward de Bono. It was introduced in his book The Five-Day Course in Thinking (1967).

Several map-coloring games are studied in combinatorial game theory. The general idea is that we are given a map with regions drawn in but with not all the regions colored. Two players, Left and Right, take turns coloring in one uncolored region per turn, subject to various constraints. The move constraints and the winning condition are features of the particular game.

Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.

Notakto is a tic-tac-toe variant, also known as neutral or impartial tic-tac-toe. The game is a combination of the games tic-tac-toe and Nim, played across one or several boards with both of the players playing the same piece. The game ends when all the boards contain a three-in-a-row of Xs, at which point the player to have made the last move loses the game. However, in this game, unlike tic-tac-toe, there will always be a player who wins any game of Notakto.

Penney's game, named after its inventor Walter Penney, is a binary (head/tail) sequence generating game between two players. Player A selects a sequence of heads and tails, and shows this sequence to player B. Player B then selects another sequence of heads and tails of the same length. Subsequently, a fair coin is tossed until either player A's or player B's sequence appears as a consecutive subsequence of the coin toss outcomes. The player whose sequence appears first wins.

A pentomino is a polyomino of order 5, that is, a polygon in the plane made of 5 equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.

Phutball is a two-player abstract strategy board game described in Elwyn Berlekamp, John Horton Conway, and Richard K. Guy's Winning Ways for your Mathematical Plays.

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling.

Racetrack is a paper and pencil game that simulates a car race, played by two or more players. The game is played on a squared sheet of paper, with a pencil line tracking each car's movement. The rules for moving represent a car with a certain inertia and physical limits on traction, and the resulting line is reminiscent of how real racing cars move. The game requires players to slow down before bends in the track, and requires some foresight and planning for successful play. The game is popular as an educational tool teaching vectors.

Rithmomachy is a highly complex, early European mathematical board game. The earliest known description of it dates from the eleventh century. A literal translation of the name is "The Battle of the Numbers". The game is much like chess, except most methods of capture depend on the numbers inscribed on each piece.

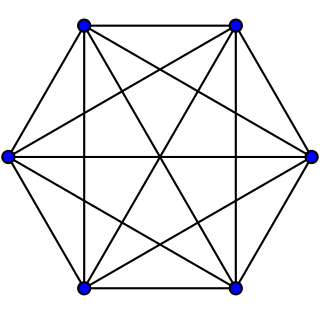
Sim is a pencil-and-paper game that is played by two players.

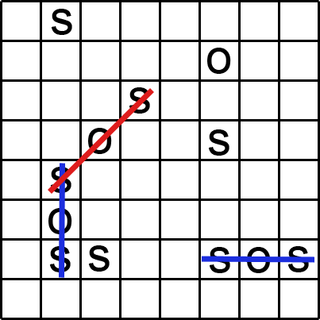
SOS is paper and pencil game for two or more players. It is similar to tic-tac-toe and dots and boxes, but has greater complexity.

Spoof is a strategy game, typically played as a gambling game, often in bars and pubs where the loser buys the other participants a round of drinks. The exact origin of the game is unknown, but one scholarly paper addressed it, and more general n-coin games, in 1959. It is an example of a zero-sum game. The version with three coins is sometimes known under the name Three Coin.

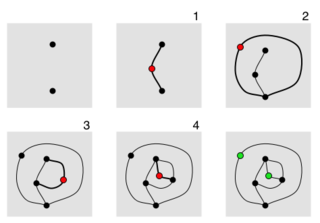
Sprouts is a paper-and-pencil game that can be enjoyed simply by both adults and children. Yet it also can be analyzed for its significant mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s. Setup is even simpler than the popular Dots and Boxes game, but game-play develops much more artistically and organically.

TacTix is a two-player strategy game invented by Piet Hein, a poet well known for dabbling in math and science. Players take turns to remove any number of contiguous pieces from a grid of playing pieces, alternating until the last piece is removed.

Tangloids is a mathematical game for two players created by Piet Hein to model the calculus of spinors.

A tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino. The corresponding polycube, called a tetracube, is a geometric shape composed of four cubes connected orthogonally.

Ultimate tic-tac-toe is a board game composed of nine tic-tac-toe boards arranged in a 3 × 3 grid. Players take turns playing in the smaller tic-tac-toe boards until one of them wins in the larger tic-tac-toe board. Compared to traditional tic-tac-toe, strategy in this game is conceptually more difficult and has proven more challenging for computers.

Wythoff's game is a two-player mathematical subtraction game, played with two piles of counters. Players take turns removing counters from one or both piles; when removing counters from both piles, the numbers of counters removed from each pile must be equal. The game ends when one person removes the last counter or counters, thus winning.