37 Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R. (compare this with Playfair's axiom, the modern version of Euclid's parallel postulate)

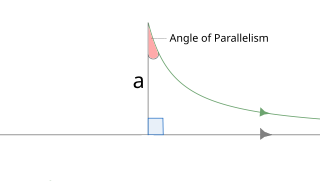
In hyperbolic geometry, the angle of parallelism , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.

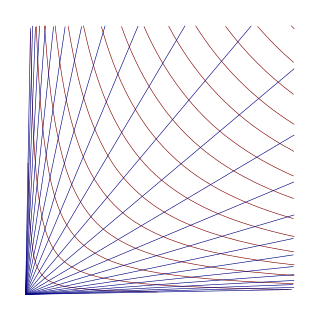
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated starting from a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga.

Apollonian sphere packing is the three-dimensional equivalent of the Apollonian gasket. The principle of construction is very similar: with any four spheres that are cotangent to each other, it is then possible to construct two more spheres that are cotangent to four of them.

In geometry, the band model is a conformal model of the hyperbolic plane. The band model employs a portion of the Euclidean plane between two parallel lines. Distance is preserved along one line through the middle of the band. Assuming the band is given by :\left|\operatorname {Im} z\right|<\pi /2\}} , the metric is given by .

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

Hyperbolic geometry is a non-Euclidean geometry where the first four axioms of Euclidean geometry are kept but the fifth axiom, the parallel postulate, is changed. The fifth axiom of hyperbolic geometry says that given a line L and a point P not on that line, there are at least two lines passing through P that are parallel to L. As in Euclidean geometry, where ancient Greek mathematicians used a compass and idealized ruler for constructions of lengths, angles, and other geometric figures, constructions can also be made in hyperbolic geometry.

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric. A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.

A gyrovector space is a mathematical concept proposed by Abraham A. Ungar for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. Ungar introduced the concept of gyrovectors that have addition based on gyrogroups instead of vectors which have addition based on groups. Ungar developed his concept as a tool for the formulation of special relativity as an alternative to the use of Lorentz transformations to represent compositions of velocities. This is achieved by introducing "gyro operators"; two 3d velocity vectors are used to construct an operator, which acts on another 3d velocity.

In mathematics, specifically in the area of hyperbolic geometry, Hilbert's arithmetic of ends is a method for endowing a geometric set, the set of ideal points or "ends" of a hyperbolic plane, with an algebraic structure as a field. It was introduced by German mathematician David Hilbert.

In mathematics, the Hjelmslev transformation is an effective method for mapping an entire hyperbolic plane into a circle with a finite radius. The transformation was invented by Danish mathematician Johannes Hjelmslev. It utilizes Nikolai Ivanovich Lobachevsky's 23rd theorem from his work Geometrical Investigations on the Theory of Parallels.

In hyperbolic geometry, a horocycle is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional example of a horosphere.

In hyperbolic geometry, a horosphere is a specific hypersurface in hyperbolic n-space. It is the boundary of a horoball, the limit of a sequence of increasing balls sharing a tangent hyperplane and its point of tangency. For n = 2 a horosphere is called a horocycle.

In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane :\ x>0,\ y>0\ \}=Q} .

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, just as the slopes of sin(t) and cos(t) are cos(t) and –sin(t), so the slopes of sinh(t) and cosh(t) are cosh(t) and +sinh(t).

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov (1987). The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.

In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman.

In mathematics, a hyperbolic space is a homogeneous space that has a constant negative curvature, where in this case the curvature is the sectional curvature. It is hyperbolic geometry in more than 2 dimensions, and is distinguished from Euclidean spaces with zero curvature that define the Euclidean geometry, and elliptic geometry that have a constant positive curvature.

A hyperbolic tree is an information visualization and graph drawing method inspired by hyperbolic geometry.

In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily a finite real number, and is a topological invariant of the link. As a link invariant, it was first studied by William Thurston in connection with his geometrization conjecture.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space and m-planes are represented by the intersections of the (m+1)-planes in Minkowski space with S+. The hyperbolic distance function admits a simple expression in this model. The hyperboloid model of the n-dimensional hyperbolic space is closely related to the Beltrami–Klein model and to the Poincaré disk model as they are projective models in the sense that the isometry group is a subgroup of the projective group.

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

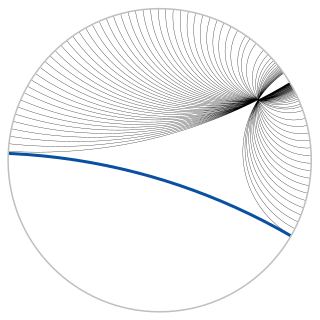
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.

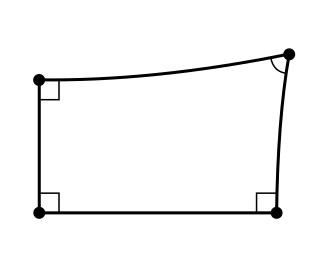
In geometry, a Lambert quadrilateral, named after Johann Heinrich Lambert, is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel postulate could be proved as a theorem. It is now known that the type of the fourth angle depends upon the geometry in which the quadrilateral exists. In hyperbolic geometry the fourth angle is acute, in Euclidean geometry it is a right angle and in elliptic geometry it is an obtuse angle.

In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line through a point not on line ; however, in the plane, two parallels may be closer to than all others.

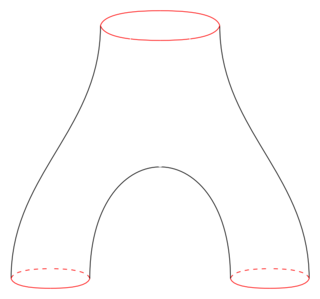
In mathematics, a pair of pants is a surface which is homeomorphic to the three-holed sphere. The name comes from considering one of the removed disks as the waist and the two others as the cuffs of a pair of pants.

In geometry, a pleated surface is roughly a surface that may have simple folds but is not crumpled in more complicated ways. More precisely, a pleated surface is an isometry from a complete hyperbolic surface S to a hyperbolic 3-fold such that every point of S is in the interior of a geodesic that is mapped to a geodesic. They were introduced by Thurston, where they were called uncrumpled surfaces.

In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which the points of the geometry are inside the unit disk, and the straight lines consist of all circular arcs contained within that disk that are orthogonal to the boundary of the disk, plus all diameters of the disk.

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.

In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.

A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclides ab omni naevo vindicatus first published in 1733, an attempt to prove the parallel postulate using the method Reductio ad absurdum.

In complex analysis, the Schwarz triangle function or Schwarz s-function is a function that conformally maps the upper half plane to a triangle in the upper half plane having lines or circular arcs for edges. Let πα, πβ, and πγ be the interior angles at the vertices of the triangle. If any of α, β, and γ are greater than zero, then the Schwarz triangle function can be given in terms of hypergeometric functions as:

In mathematics, the special linear group SL(2,R) or SL2(R) is the group of 2 × 2 real matrices with determinant one:

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

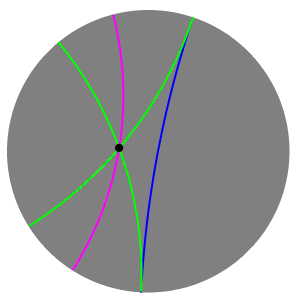
In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel.