38 Analytic geometry

In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In mathematics, a 3-sphere, or glome, is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends.

In geometry a circular section is a circle on a quadric surface. It is a special plane section of the quadric, as this circle is the intersection with the quadric of the plane containing the circle.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the x-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.

In mathematics, the cross product or vector product is a binary operation on two vectors in three-dimensional space , and is denoted by the symbol . Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.

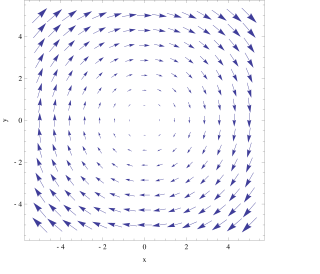
In vector calculus, the curl is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.

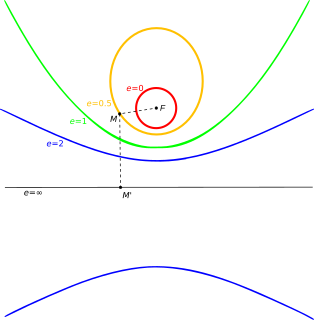
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.

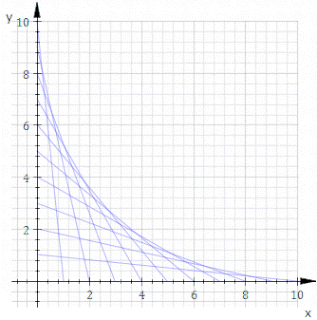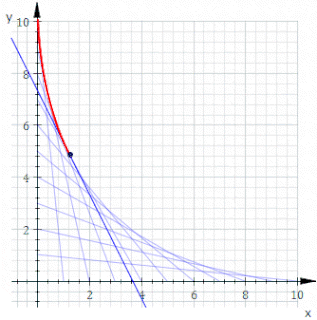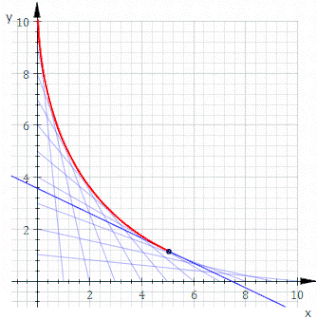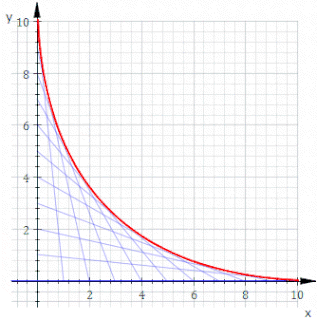
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

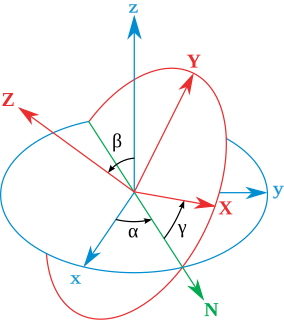
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.

Galois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field. More narrowly, a Galois geometry may be defined as a projective space over a finite field.

The Hesse normal form named after Otto Hesse, is an equation used in analytic geometry, and describes a line in or a plane in Euclidean space or a hyperplane in higher dimensions. It is primarily used for calculating distances.

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave to convex, or vice versa.

In geometry and group theory, a lattice in is a subgroup of the additive group which is isomorphic to the additive group , and which spans the real vector space . In other words, for any basis of , the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice. A lattice may be viewed as a regular tiling of a space by a primitive cell.

In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects, which are often described in terms of two points or referred to using a single letter.

In topography, the line of greatest slope is a curve following the steepest slope. In mountain biking and skiing, the line of greatest slope is sometimes called the fall line.

In analytic geometry, a line and a sphere can intersect in three ways:No intersection at all Intersection in exactly one point Intersection in two points.

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In mathematics, orientation is a geometric notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary finite dimension. In this setting, the orientation of an ordered basis is a kind of asymmetry that makes a reflection impossible to replicate by means of a simple rotation. Thus, in three dimensions, it is impossible to make the left hand of a human figure into the right hand of the figure by applying a rotation alone, but it is possible to do so by reflecting the figure in a mirror. As a result, in the three-dimensional Euclidean space, the two possible basis orientations are called right-handed and left-handed.

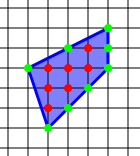
Given a simple polygon constructed on a grid of equal-distanced points such that all the polygon's vertices are grid points, Pick's theorem provides a simple formula for calculating the area A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the number b of lattice points on the boundary placed on the polygon's perimeter:

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle O of radius r is defined by.

In geometry, the radical axis of two non-concentric circles is a line defined from the two circles, perpendicular to the line connecting the centers of the circles. If the circles cross, their radical axis is the line through their two crossing points, and if they are tangent, it is their line of tangency. For two disjoint circles, the radical axis is the locus of points at which tangents drawn to both circles have equal lengths.

In geometry, a radiodrome is the pursuit curve followed by a point that is pursuing another linearly-moving point. The term is derived from the Greek words ῥᾴδιος, rhā́idios, 'easier' and δρόμος, drómos, 'running'. The classic form of a radiodrome is known as the "dog curve"; this is the path a dog follows when it swims across a stream with a current after something it has spotted on the other side. Because the dog drifts with the current, it will have to change its heading; it will also have to swim further than if it had taken the optimal heading. This case was described by Pierre Bouguer in 1732.

In mathematics, a real coordinate space of dimension n, written Rn or ℝn, is a coordinate space over the real numbers. This means that it is the set of the n-tuples of real numbers. With component-wise addition and scalar multiplication, it is a real vector space.

In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero, but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function has a critical point at that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the -direction.

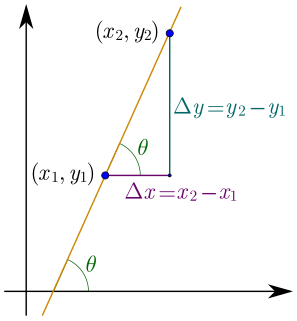
In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but its earliest use in English appears in O'Brien (1844) who wrote the equation of a straight line as "y = mx + b" and it can also be found in Todhunter (1888) who wrote it as "y = mx + c".

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f ) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis.

Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.

Translation surface (differential geometry)

In differential geometry a translation surface is a surface that is generated by translations:For two space curves with a common point , the curve is shifted such that point is moving on . By this procedure curve generates a surface: the translation surface.

In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as S1 because it is a one-dimensional unit n-sphere.

In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length