38 Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers or defined as generalizations of the integers.

In mathematics, an arithmetic group is a group obtained as the integer points of an algebraic group, for example They arise naturally in the study of arithmetic properties of quadratic forms and other classical topics in number theory. They also give rise to very interesting examples of Riemannian manifolds and hence are objects of interest in differential geometry and topology. Finally, these two topics join in the theory of automorphic forms which is fundamental in modern number theory.

In mathematics, the Barnes G-function G(z) is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function.

In mathematics, the Bernoulli polynomials, named after Jacob Bernoulli, combine the Bernoulli numbers and binomial coefficients. They are used for series expansion of functions, and with the Euler–MacLaurin formula.

In mathematics, in number theory, a Bhargava cube is a configuration consisting of eight integers placed at the eight corners of a cube. This configuration was extensively used by Manjul Bhargava, a Canadian-American Fields Medal winning mathematician, to study the composition laws of binary quadratic forms and other such forms. To each pair of opposite faces of a Bhargava cube one can associate an integer binary quadratic form thus getting three binary quadratic forms corresponding to the three pairs of opposite faces of the Bhargava cube. These three quadratic forms all have the same discriminant and Manjul Bhargava proved that their composition in the sense of Gauss is the identity element in the associated group of equivalence classes of primitive binary quadratic forms. Using this property as the starting point for a theory of composition of binary quadratic forms Manjul Bhargava went on to define fourteen different composition laws using a cube.

In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of (strictly) positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Every integer has finitely many distinct compositions. Negative numbers do not have any compositions, but 0 has one composition, the empty sequence. Each positive integer n has 2n−1 distinct compositions.

In number theory, the crank of a partition of an integer is a certain integer associated with the partition. The term was first introduced without a definition by Freeman Dyson in a 1944 paper published in Eureka, a journal published by the Mathematics Society of Cambridge University. Dyson then gave a list of properties this yet-to-be-defined quantity should have. In 1988, George E. Andrews and Frank Garvan discovered a definition for the crank satisfying the properties hypothesized for it by Dyson.

In arithmetic and algebra, the cube of a number n is its third power, that is, the result of multiplying three instances of n together. The cube of a number or any other mathematical expression is denoted by a superscript 3, for example 23 = 8 or (x + 1)3.

The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24. It is notable for having had a revolutionary impact on the field of number theory as it not only made the field truly rigorous and systematic but also paved the path for modern number theory. In this book Gauss brought together and reconciled results in number theory obtained by mathematicians such as Fermat, Euler, Lagrange, and Legendre and added many profound and original results of his own.

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

For any given prime number , a p-adic fraction or p-adic rational is a rational number whose denominator, when the ratio is in minimal (coprime) terms, is a power of , i.e., a number of the form where a is an integer and b is a natural number. These are precisely the numbers possessing a finite base-p positional numeral system expansion.

An Egyptian fraction is a finite sum of distinct unit fractions, such as

In number theory, the Elkies trinomial curves are certain hyperelliptic curves constructed by Noam Elkies which have the property that rational points on them correspond to trinomial polynomials giving an extension of Q with particular Galois groups.

In mathematics, the Euler function is given by

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.

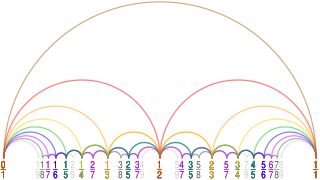
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions, either between 0 and 1, or without this restriction, which when in lowest terms have denominators less than or equal to n, arranged in order of increasing size.

In mathematics, a Golomb ruler is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its order, and the largest distance between two of its marks is its length. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values.

Günter Harder is a German mathematician, specializing in arithmetic geometry and number theory.

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

History of the Theory of Numbers is a three-volume work by L. E. Dickson summarizing work in number theory up to about 1920. The style is unusual in that Dickson mostly just lists results by various authors, with little further discussion. The central topic of quadratic reciprocity and higher reciprocity laws is barely mentioned; this was apparently going to be the topic of a fourth volume that was never written.

The Journal of Number Theory is a bimonthly peer-reviewed scientific journal covering all aspects of number theory. The journal was established in 1969 by R.P. Bambah, P. Roquette, A. Ross, A. Woods, and H. Zassenhaus. It is currently published monthly by Elsevier and the editor-in-chief is Dorian Goldfeld. According to the Journal Citation Reports, the journal has a 2017 impact factor of 0.774.

In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero. However, some authors define lcm(a,0) as 0 for all a, which is the result of taking the lcm to be the least upper bound in the lattice of divisibility.

In mathematics, the natural numbers are those used for counting and ordering. In common mathematical terminology, words colloquially used for counting are "cardinal numbers", and words used for ordering are "ordinal numbers". The natural numbers can, at times, appear as a convenient set of codes ; that is, as what linguists call nominal numbers, forgoing many or all of the properties of being a number in a mathematical sense. The set of natural numbers is often denoted by the symbol .

In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers.

In mathematics, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a different way from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of "closeness" or absolute value. In particular, two p-adic numbers are considered to be close when their difference is divisible by a high power of p: the higher the power, the closer they are. This property enables p-adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory – including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles.

In mathematics, Paley graphs are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yield an infinite family of symmetric conference matrices. Paley graphs allow graph-theoretic tools to be applied to the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally.

In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. For example, 4 can be partitioned in five distinct ways:4 3 + 1 2 + 2 2 + 1 + 1 1 + 1 + 1 + 1

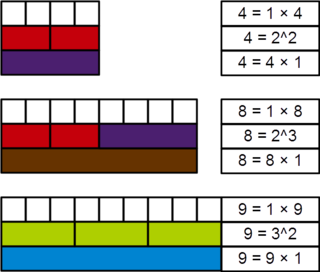
In mathematics, a perfect power is a positive integer that can be resolved into equal factors, and whose root can be exactly extracted, i.e., a positive integer that can be expressed as an integer power of another positive integer. More formally, n is a perfect power if there exist natural numbers m > 1, and k > 1 such that mk = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers.

Primecoin is a cryptocurrency that implements a proof-of-work system that searches for chains of prime numbers.

In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers. Due to its subtlety, it has many formulations, but the most standard statement is:

In mathematics, particularly in the fields of number theory and combinatorics, the rank of a partition of a positive integer is a certain integer associated with the partition. In fact at least two different definitions of rank appear in the literature. The first definition, with which most of this article is concerned, is that the rank of a partition is the number obtained by subtracting the number of parts in the partition from the largest part in the partition. The concept was introduced by Freeman Dyson in a paper published in the journal Eureka. It was presented in the context of a study of certain congruence properties of the partition function discovered by the Indian mathematical genius Srinivasa Ramanujan. A different concept, sharing the same name, is used in combinatorics, where the rank is taken to be the size of the Durfee square of the partition.

In mathematics, a solenoid is a compact connected topological space that may be obtained as the inverse limit of an inverse system of topological groups and continuous homomorphisms(Si, fi), fi: Si+1 → Si, i ≥ 0,

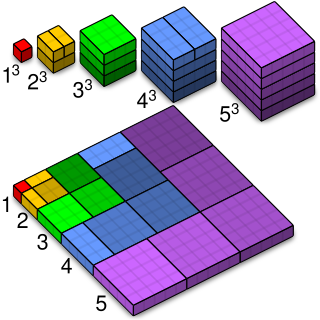
In number theory, the sum of the first n cubes is the square of the nth triangular number. That is,

In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond one-for-one to the positive rational numbers, whose values are ordered from the left to the right as in a search tree.

In mathematics, the supernatural numbers, sometimes called generalized natural numbers or Steinitz numbers, are a generalization of the natural numbers. They were used by Ernst Steinitz in 1910 as a part of his work on field theory.

In number theory, Sylvester's sequence is an integer sequence in which each term of the sequence is the product of the previous terms, plus one. The first few terms of the sequence are2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443.

In mathematics, the nth taxicab number, typically denoted Ta(n) or Taxicab(n), also called the nth Hardy–Ramanujan number, is defined as the smallest integer that can be expressed as a sum of two positive integer cubes in n distinct ways. The most famous taxicab number is 1729 = Ta(2) = 13 + 123 = 93 + 103.

In number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other mathematicians had considered similar problems around the same time. One closely related problem drops the assumption of properness of the divisor, and will be called the improper Znám problem hereafter.