39 NP complete problems

In computational complexity theory, a problem is NP-complete when:A nondeterministic Turing machine can solve it in polynomial-time. A deterministic Turing machine can solve it in large time complexity classes and can verify its solutions in polynomial time. It can be used to simulate any other problem with similar solvability.

In the mathematical discipline of graph theory, a 3-dimensional matching is a generalization of bipartite matching to 3-partite hypergraphs. Finding a largest 3-dimensional matching is a well-known NP-hard problem in computational complexity theory.

The 15 puzzle is a sliding puzzle that consists of a frame of numbered square tiles in random order with one tile missing. The puzzle also exists in other sizes, particularly the smaller 8 puzzle. If the size is 3×3 tiles, the puzzle is called the 8 puzzle or 9 puzzle, and if 4×4 tiles, the puzzle is called the 15 puzzle or 16 puzzle named, respectively, for the number of tiles and the number of spaces. The goal of the puzzle is to place the tiles in order by making sliding moves that use the empty space.

The Battleship puzzle is a logic puzzle based on the Battleship guessing game. It and its variants have appeared in several puzzle contests, including the World Puzzle Championship, and puzzle magazines, such as Games magazine.

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

In graph theory, a dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is adjacent to at least one member of D. The domination number γ(G) is the number of vertices in a smallest dominating set for G.

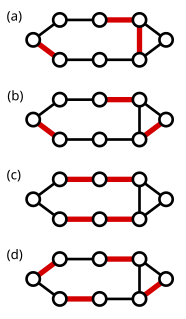
In graph theory, an edge dominating set for a graph G = (V, E) is a subset D ⊆ E such that every edge not in D is adjacent to at least one edge in D. An edge dominating set is also known as a line dominating set. Figures (a)–(d) are examples of edge dominating sets.

A feedback arc set (FAS) or feedback edge set is a set of edges which, when removed from the graph, leaves an acyclic graph. Put another way, it is a set containing at least one edge of every cycle in the graph. In graph theory, a directed graph may contain directed cycles, a closed one-way path of edges. In some applications, such cycles are undesirable, and we wish to eliminate them and obtain a directed acyclic graph (DAG). One way to do this is simply to drop edges from the graph to break the cycles.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a Hamiltonian path that is a cycle. Determining whether such paths and cycles exist in graphs is the Hamiltonian path problem, which is NP-complete.

Hashiwokakero is a type of logic puzzle published by Nikoli. It has also been published in English under the name Bridges or Chopsticks. It has also appeared in The Times under the name Hashi. In France, Denmark, the Netherlands, and Belgium it is published under the name Ai-Ki-Ai.

Hitori is a type of logic puzzle published by Nikoli.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set of vertices such that for every two vertices in , there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . The size of an independent set is the number of vertices it contains. Independent sets have also been called internally stable sets.

Instant Insanity is the name given by Parker Brothers to their 1967 version of a puzzle which has existed since antiquity, and which has been marketed many toy and puzzle makers under a variety of names, including: Devil's Dice (Pressman); DamBlocks (Schaper); Logi-Qubes (Schaeffer); Logi Cubes (ThinkinGames); Daffy Dots (Reiss); Those Blocks (Austin); PsykoNosis, and many others.

Kakuro or Kakkuro or Kakoro is a kind of logic puzzle that is often referred to as a mathematical transliteration of the crossword. Kakuro puzzles are regular features in many math-and-logic puzzle publications across the world. In 1966, Canadian Jacob E. Funk, an employee of Dell Magazines, came up with the original English name Cross Sums and other names such as Cross Addition have also been used, but the Japanese name Kakuro, abbreviation of Japanese kasan kurosu, seems to have gained general acceptance and the puzzles appear to be titled this way now in most publications. The popularity of Kakuro in Japan is immense, second only to Sudoku among Nikoli's famed logic-puzzle offerings.

The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. The problem often arises in resource allocation where the decision makers have to choose from a set of non-divisible projects or tasks under a fixed budget or time constraint, respectively.

Light Up, also called Akari, is a binary-determination logic puzzle published by Nikoli. As of 2011, three books consisting entirely of Light Up puzzles have been published by Nikoli.

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences. It differs from the longest common substring problem: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in computational linguistics and bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.

Mastermind or Master Mind is a code-breaking game for two players. The modern game with pegs was invented in 1970 by Mordecai Meirowitz, an Israeli postmaster and telecommunications expert. It resembles an earlier pencil and paper game called Bulls and Cows that may date back a century.

Masyu is a type of logic puzzle designed and published by Nikoli. The purpose of its creation was to present a puzzle that uses no numbers or letters and yet retains depth and aesthetics.

For a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets S and T, such that the number of edges between the set S and the set T is as large as possible. The problem of finding a maximum cut in a graph is known as the Max-Cut Problem.

Minesweeper is a single-player puzzle video game. The objective of the game is to clear a rectangular board containing hidden "mines" or bombs without detonating any of them, with help from clues about the number of neighboring mines in each field. The game originates from the 1960s, and it has been written for many computing platforms in use today. It has many variations and offshoots.

In graph theory and theoretical computer science, the monochromatic triangle problem is an algorithmic problem on graphs, in which the goal is to partition the edges of a given graph into two triangle-free subgraphs. It is NP-complete but fixed-parameter tractable on graphs of bounded treewidth.

Nonograms, also known as Paint by Numbers, Picross, Griddlers, Pic-a-Pix, and various other names, are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the side of the grid to reveal a hidden picture. In this puzzle type, the numbers are a form of discrete tomography that measures how many unbroken lines of filled-in squares there are in any given row or column. For example, a clue of "4 8 3" would mean there are sets of four, eight, and three filled squares, in that order, with at least one blank square between successive sets.

Nurikabe is a binary determination puzzle named for Nurikabe, an invisible wall in Japanese folklore that blocks roads and delays foot travel. Nurikabe was apparently invented and named by Nikoli; other names for the puzzle include Cell Structure and Islands in the Stream.

In computer science, the planar 3-satisfiability problem is an extension of the classical Boolean 3-satisfiability problem to a planar incidence graph. In other words, it asks whether the variables of a given Boolean formula—whose incidence graph consisting of variables and clauses can be embedded on a plane—can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

Quadrel is a puzzle video game developed by Loriciels and released during June 1991. It was released for MS-DOS, Amiga, Atari ST and Amstrad CPC

In graph theory, a branch of mathematics, a radio coloring of an undirected graph is a form of graph coloring in which one assigns positive integer labels to the graphs such that the labels of adjacent vertices differ by at least two, and the labels of vertices at distance two from each other differ by at least one. Radio coloring was first studied by Griggs & Yeh (1992), under a different name, L(2,1)-labeling. It was called radio coloring by Frank Harary because it models the problem of channel assignment in radio broadcasting, while avoiding electromagnetic interference between radio stations that are near each other both in the graph and in their assigned channel frequencies.

SameGame (さめがめ) is a tile-matching puzzle originally released under the name Chain Shot! in 1985 by Kuniaki Moribe (Morisuke). It has since been ported to numerous computer platforms, handheld devices, and even TiVo, with new versions as of 2016.

Shakashaka (シャカシャカ) is a logic puzzle developed by publisher Nikoli. The objective is to fill the white squares in a given grid with a pattern of triangles such that each white area in the resulting grid has a rectangular shape. Furthermore, each black square in the grid marked with a number must be orthogonally adjacent to the specified number of triangles.

Slitherlink is a logic puzzle developed by publisher Nikoli.

The Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.

Sudoku is a logic-based, combinatorial number-placement puzzle. In classic sudoku, the objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

Tetris is a tile-matching video game created by Russian software engineer Alexey Pajitnov in 1984. It has been published by several companies, most prominently during a dispute over the appropriation of the rights in the late 1980s. After a significant period of publication by Nintendo, the rights reverted to Pajitnov in 1996, who co-founded The Tetris Company with Henk Rogers to manage licensing.

The travelling salesman problem asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.

The vehicle rescheduling problem (VRSP) is a combinatorial optimization and integer programming problem seeking to service customers on a trip after change of schedule such as vehicle break down or major delay. Proposed by Li, Mirchandani and Borenstein in 2007, the VRSP is an important problem in the fields of transportation and logistics.

The vehicle routing problem (VRP) is a combinatorial optimization and integer programming problem which asks "What is the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers?". It generalises the well-known travelling salesman problem (TSP). It first appeared in a paper by George Dantzig and John Ramser in 1959, in which the first algorithmic approach was written and was applied to petrol deliveries. Often, the context is that of delivering goods located at a central depot to customers who have placed orders for such goods. The objective of the VRP is to minimize the total route cost. In 1964, Clarke and Wright improved on Dantzig and Ramser's approach using an effective greedy approach called the savings algorithm.

In the mathematical discipline of graph theory, a vertex cover of a graph is a set of vertices that includes at least one endpoint of every edge of the graph. The problem of finding a minimum vertex cover is a classical optimization problem in computer science and is a typical example of an NP-hard optimization problem that has an approximation algorithm. Its decision version, the vertex cover problem, was one of Karp's 21 NP-complete problems and is therefore a classical NP-complete problem in computational complexity theory. Furthermore, the vertex cover problem is fixed-parameter tractable and a central problem in parameterized complexity theory.