40 Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.

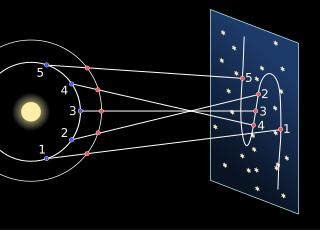
Apparent retrograde motion is the apparent motion of a planet in a direction opposite to that of other bodies within its system, as observed from a particular vantage point. Direct motion or prograde motion is motion in the same direction as other bodies.

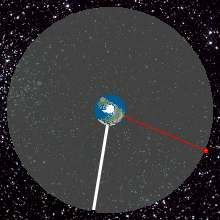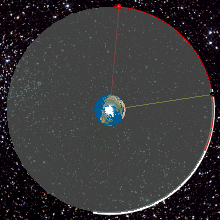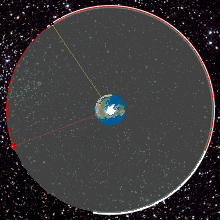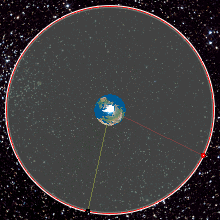
The beta angle is a measurement that is used most notably in orbital spaceflight. The beta angle determines the percentage of time that a satellite in low Earth orbit (LEO) spends in direct sunlight, absorbing solar energy. The term is defined as the angle between the orbital plane of the satellite and the vector to the Sun. The beta angle is the smaller of the two angles between the Sun vector and the plane of the object's orbit. The beta angle does not define a unique orbital plane; all satellites in orbit with a given beta angle at a given altitude have the same exposure to the Sun, even though they may be orbiting in completely different planes around Earth.

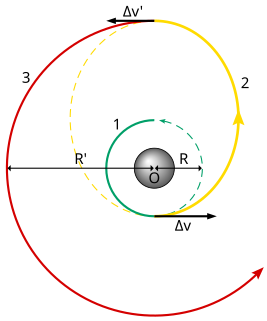
In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.

In astrodynamics and aerospace, a delta-v budget is an estimate of the total change in velocity (delta-v) required for a space mission. It is calculated as the sum of the delta-v required to perform each propulsive maneuver needed during the mission. As input to the Tsiolkovsky rocket equation, it determines how much propellant is required for a vehicle of given mass and propulsion system.

In physics, escape velocity is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a massive body, that is, to eventually reach an infinite distance from it. Escape velocity rises with the body's mass and falls with the escaping object's distance from its center. The escape velocity thus depends on how far the object has already travelled, and its calculation at a given distance takes into account the fact that without new acceleration it will slow down as it travel, due to the massive body's gravity-- but it will never quite slow to a stop.

Flight dynamics (spacecraft)

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

A geostationary orbit, also referred to as a geosynchronous equatorial orbit (GEO), is a circular geosynchronous orbit 35,786 kilometres above Earth's equator and following the direction of Earth's rotation.

A geosynchronous transfer orbit or geostationary transfer orbit (GTO) is a type of geocentric orbit. Satellites which are destined for geosynchronous (GSO) or geostationary orbit (GEO) are (almost) always put into a GTO as an intermediate step for reaching their final orbit.

A graveyard orbit, also called a junk orbit or disposal orbit, is an orbit that lies away from common operational orbits. One significant graveyard orbit is a supersynchronous orbit well above geosynchronous orbit. Some satellites are moved into such orbits at the end of their operational life to reduce the probability of colliding with operational spacecraft and generating space debris.

In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense.

A ground track or ground trace is the path on the surface of a planet directly below an aircraft or satellite. In the case of a satellite, it is the projection of the satellite's orbit onto the surface of the Earth.

A heliocentric orbit is an orbit around the barycenter of the Solar System, which is usually located within or very near the surface of the Sun. All planets, comets, and asteroids in the Solar System, and the Sun itself are in such orbits, as are many artificial probes and pieces of debris. The moons of planets in the Solar System, by contrast, are not in heliocentric orbits, as they orbit their respective planet.

In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different radii around a central body in the same plane. The Hohmann transfer often uses the lowest possible amount of propellant in traveling between these orbits, but bi-elliptic transfers can beat it in some cases.

The International Berthing and Docking Mechanism (IBDM) is the European androgynous low impact docking mechanism that is capable of docking and berthing large and small spacecraft. The development of the IBDM is under ESA contract with QinetiQ Space as prime contractor.

The Interplanetary Transport Network (ITN) is a collection of gravitationally determined pathways through the Solar System that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space can be redirected using little or no energy. These points have the peculiar property of allowing objects to orbit around them, despite lacking an object to orbit. While it would use little energy, transport along the network would take a long time.

A low-energy transfer, or low-energy trajectory, is a route in space that allows spacecraft to change orbits using very little fuel. These routes work in the Earth–Moon system and also in other systems, such as between the moons of Jupiter. The drawback of such trajectories is that they take longer to complete than higher-energy (more-fuel) transfers, such as Hohmann transfer orbits.

In aerospace engineering, mass ratio is a measure of the efficiency of a rocket. It describes how much more massive the vehicle is with propellant than without; that is, the ratio of the rocket's wet mass to its dry mass. A more efficient rocket design requires less propellant to achieve a given goal, and would therefore have a lower mass ratio; however, for any given efficiency a higher mass ratio typically permits the vehicle to achieve higher delta-v.

Minimum orbit intersection distance (MOID) is a measure used in astronomy to assess potential close approaches and collision risks between astronomical objects. It is defined as the distance between the closest points of the osculating orbits of two bodies. Of greatest interest is the risk of a collision with Earth. Earth MOID is often listed on comet and asteroid databases such as the JPL Small-Body Database. MOID values are also defined with respect to other bodies as well: Jupiter MOID, Venus MOID and so on.

In astronautics, a powered flyby, or Oberth maneuver, is a maneuver in which a spacecraft falls into a gravitational well and then uses its engines to further accelerate as it is falling, thereby achieving additional speed. The resulting maneuver is a more efficient way to gain kinetic energy than applying the same impulse outside of a gravitational well. The gain in efficiency is explained by the Oberth effect, wherein the use of a reaction engine at higher speeds generates a greater change in mechanical energy than its use at lower speeds. In practical terms, this means that the most energy-efficient method for a spacecraft to burn its engine is at the lowest possible orbital periapsis, when its orbital velocity is greatest. In some cases, it is even worth spending fuel on slowing the spacecraft into a gravity well to take advantage of the efficiencies of the Oberth effect. The maneuver and effect are named after the person who first described them in 1927, Hermann Oberth, an Austro-Hungarian-born German physicist and a founder of modern rocketry.

In physics, an orbit is the gravitationally curved trajectory of an object, such as the trajectory of a planet around a star or a natural satellite around a planet. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

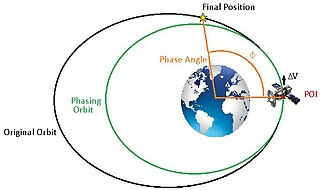
In astrodynamics, orbit phasing is the adjustment of the time-position of spacecraft along its orbit, usually described as adjusting the orbiting spacecraft's true anomaly. Orbital phasing is primarily used in scenarios where a spacecraft in a given orbit must be moved to a different location within the same orbit. The change in position within the orbit is usually defined as the phase angle, ϕ, and is the change in true anomaly required between the spacecraft's current position to the final position.

Orbital Mechanics for Engineering Students is an aerospace engineering textbook by Howard D. Curtis, in its fourth edition as of 2019. The book provides an introduction to orbital mechanics, while assuming an undergraduate-level background in physics, rigid body dynamics, differential equations, and linear algebra.

In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit that it would have around its central body if perturbations were absent. That is, it is the orbit that coincides with the current orbital state vectors.

A pass, in spaceflight and satellite communications, is the period in which a satellite or other spacecraft is above the local horizon and available for radio communication with a particular ground station, satellite receiver, or relay satellite. The beginning of a pass is termed acquisition of signal; the end of a pass is termed loss of signal. The point at which a spacecraft comes closest to a ground observer is the time of closest approach.

In aerospace engineering, payload fraction is a common term used to characterize the efficiency of a particular design. Payload fraction is calculated by dividing the weight of the payload by the takeoff weight of aircraft. Fuel represents a considerable amount of the overall takeoff weight, and for shorter trips it is quite common to load less fuel in order to carry a lighter load. For this reason the useful load fraction calculates a similar number, but based on the combined weight of the payload and fuel together.

A polar orbit is one in which a satellite passes above or nearly above both poles of the body being orbited on each revolution. It therefore has an inclination of 90 degrees to the body's equator. A satellite in a polar orbit will pass over the equator at a different longitude on each of its orbits.

A porkchop plot (also pork-chop plot) is a chart that shows contours of equal characteristic energy (C3) against combinations of launch date and arrival date for a particular interplanetary flight.

In aerospace engineering, the propellant mass fraction is the portion of a vehicle's mass which does not reach the destination, usually used as a measure of the vehicle's performance. In other words, the propellant mass fraction is the ratio between the propellant mass and the initial mass of the vehicle. In a spacecraft, the destination is usually an orbit, while for aircraft it is their landing location. A higher mass fraction represents less weight in a design. Another related measure is the payload fraction, which is the fraction of initial weight that is payload. It can be applied to a vehicle, a stage of a vehicle or to a rocket propulsion system.

In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.

A space rendezvous is a set of orbital maneuvers during which two spacecraft, one of which is often a space station, arrive at the same orbit and approach to a very close distance. Rendezvous requires a precise match of the orbital velocities and position vectors of the two spacecraft, allowing them to remain at a constant distance through orbital station-keeping. Rendezvous may or may not be followed by docking or berthing, procedures which bring the spacecraft into physical contact and create a link between them.

In the gravitational two-body problem, the specific orbital energy of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy, divided by the reduced mass. According to the orbital energy conservation equation, it does not vary with time:

A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region around a celestial body where the primary gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by.

A star tracker is an optical device that measures the positions of stars using photocells or a camera. As the positions of many stars have been measured by astronomers to a high degree of accuracy, a star tracker on a satellite or spacecraft may be used to determine the orientation of the spacecraft with respect to the stars. In order to do this, the star tracker must obtain an image of the stars, measure their apparent position in the reference frame of the spacecraft, and identify the stars so their position can be compared with their known absolute position from a star catalog. A star tracker may include a processor to identify stars by comparing the pattern of observed stars with the known pattern of stars in the sky.

A sun sensor is a navigational instrument used by spacecraft to detect the position of the sun. Sun sensors are used for attitude control, solar array pointing, gyro updating, and fail-safe recovery.

A trans-lunar injection (TLI) is a propulsive maneuver used to set a spacecraft on a trajectory that will cause it to arrive at the Moon.

In orbital mechanics a transfer orbit is an intermediate elliptical orbit that is used to move a satellite or other object from one circular, or largely circular, orbit to another.

Transposition, docking, and extraction was a maneuver performed during Apollo lunar landing missions from 1969 to 1972, to withdraw the Apollo Lunar Module (LM) from its adapter housing which secured it to the Saturn V launch vehicle upper stage and protected it from the aerodynamic stresses of launch. The maneuver involved the command module pilot separating the Apollo Command and Service Module (CSM) from the adapter, turning the CSM around, and docking its nose to the Lunar Module, then pulling the combined spacecraft away from the upper stage. It was performed shortly after the trans-lunar injection maneuver that placed the Apollo spacecraft on a three-day trajectory to the Moon. The docking created a continuous, pressurized tunnel which permitted the astronauts to transfer internally between the CSM and the LM.

The Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.