W

In the mathematical discipline of graph theory, a 3-dimensional matching is a generalization of bipartite matching to 3-partite hypergraphs. Finding a largest 3-dimensional matching is a well-known NP-hard problem in computational complexity theory.

W

Alignments of random points in a plane can be demonstrated by statistics to be counter-intuitively easy to find when a large number of random points are marked on a bounded flat surface. This has been put forward as a demonstration that ley lines and other similar mysterious alignments believed by some to be phenomena of deep significance might exist solely due to chance alone, as opposed to the supernatural or anthropological explanations put forward by their proponents. The topic has also been studied in the fields of computer vision and astronomy.

W

In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc.. These intersection subspaces of A are also called the flats of A. The intersection semilattice L(A) is partially ordered by reverse inclusion.

W

The Dissertatio de arte combinatoria is an early work by Gottfried Leibniz published in 1666 in Leipzig. It is an extended version of his first doctoral dissertation, written before the author had seriously undertaken the study of mathematics. The booklet was reissued without Leibniz' consent in 1690, which prompted him to publish a brief explanatory notice in the Acta Eruditorum. During the following years he repeatedly expressed regrets about its being circulated as he considered it immature. Nevertheless it was a very original work and it provided the author the first glimpse of fame among the scholars of his time.

W

In the mathematical field of combinatorics, a bent function is a special type of Boolean function; so called as they are as different as possible from all linear functions and from all affine functions. This makes the bent functions naturally hard to approximate. Bent functions were defined and named in the 1960s by Oscar Rothaus in research not published until 1976. They have been extensively studied for their applications in cryptography, but have also been applied to spread spectrum, coding theory, and combinatorial design. The definition can be extended in several ways, leading to different classes of generalized bent functions that share many of the useful properties of the original.

W

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n, and is given by the formula

W

In biotechnology, combinatorial biology is the creation of a large number of compounds through technologies such as phage display. Similar to combinatorial chemistry, compounds are produced by biosynthesis rather than organic chemistry. This process was developed independently by Richard A. Houghten and H. Mario Geysen in the 1980s. Combinatorial biology allows the generation and selection of the large number of ligands for high-throughput screening.

W

In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of (strictly) positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Every integer has finitely many distinct compositions. Negative numbers do not have any compositions, but 0 has one composition, the empty sequence. Each positive integer n has 2n−1 distinct compositions.

W

In number theory, the crank of a partition of an integer is a certain integer associated with the partition. The term was first introduced without a definition by Freeman Dyson in a 1944 paper published in Eureka, a journal published by the Mathematics Society of Cambridge University. Dyson then gave a list of properties this yet-to-be-defined quantity should have. In 1988, George E. Andrews and Frank Garvan discovered a definition for the crank satisfying the properties hypothesized for it by Dyson.

W

In mathematics, a cyclic order is a way to arrange a set of objects in a circle. Unlike most structures in order theory, a cyclic order is not modeled as a binary relation, such as "a < b". One does not say that east is "more clockwise" than west. Instead, a cyclic order is defined as a ternary relation [a, b, c], meaning "after a, one reaches b before c". For example, [June, October, February]. A ternary relation is called a cyclic order if it is cyclic, asymmetric, transitive, and total. Dropping the "total" requirement results in a partial cyclic order.

W

In combinatorial mathematics, a De Bruijn torus, named after Nicolaas Govert de Bruijn, is an array of symbols from an alphabet that contains every m-by-n matrix exactly once. It is a torus because the edges are considered wraparound for the purpose of finding matrices. Its name comes from the De Bruijn sequence, which can be considered a special case where n is 1.

W

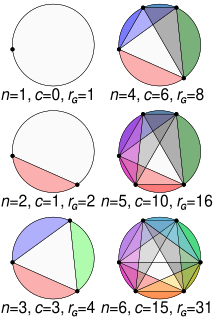
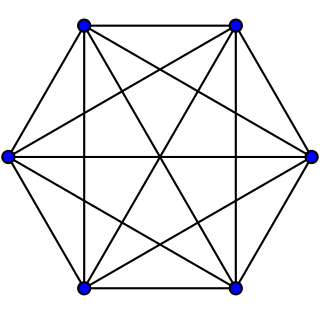
In geometry, the problem of dividing a circle into areas by means of an inscribed polygon with n sides in such a way as to maximise the number of areas created by the edges and diagonals, sometimes called Moser's circle problem, has a solution by an inductive method. The greatest possible number of regions, rG = + + 1, giving the sequence 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, .... Though the first five terms match the geometric progression 2n − 1, it diverges at n = 6, showing the risk of generalising from only a few observations.

W

In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.

W

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.

W

In statistics and combinatorial mathematics, group testing is any procedure that breaks up the task of identifying certain objects into tests on groups of items, rather than on individual ones. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that can be applied to a wide range of practical applications and is an active area of research today.

W

In mathematics, an abstract system consisting of two types of objects and a single relationship between these types of objects is called an incidence structure. Consider the points and lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the relation of which points are on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane.

W

In computer science and discrete mathematics, a sequence has an inversion where two of its elements are out of their natural order.

W

In computer science and mathematics, the Josephus problem is a theoretical problem related to a certain counting-out game.

W

Athanasius Kircher was a German Jesuit scholar and polymath who published around 40 major works, most notably in the fields of comparative religion, geology, and medicine. Kircher has been compared to fellow Jesuit Roger Boscovich and to Leonardo da Vinci for his enormous range of interests, and has been honoured with the title "Master of a Hundred Arts". He taught for more than 40 years at the Roman College, where he set up a wunderkammer. A resurgence of interest in Kircher has occurred within the scholarly community in recent decades.

W

In mathematics, Ky Fan's lemma (KFL) is a combinatorial lemma about labellings of triangulations. It is a generalization of Tucker's lemma. It was proved by Ky Fan in 1952.

W

In combinatorial mathematics, a Langford pairing, also called a Langford sequence, is a permutation of the sequence of 2n numbers 1, 1, 2, 2, ..., n, n in which the two 1s are one unit apart, the two 2s are two units apart, and more generally the two copies of each number k are k units apart. Langford pairings are named after C. Dudley Langford, who posed the problem of constructing them in 1958.

W

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences. It differs from the longest common substring problem: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in computational linguistics and bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.

W

In computer science, the longest repeated substring problem is the problem of finding the longest substring of a string that occurs at least twice.

W

A Musikalisches Würfelspiel was a system for using dice to randomly generate music from precomposed options. These games were quite popular throughout Western Europe in the 18th century. Several different games were devised, some that did not require dice, but merely choosing a random number.

W

In mathematics, in the area of discrete geometry, the no-three-in-line problem asks for the maximum number of points that can be placed in the n × n grid so that no three points are collinear. This number is at most 2n, since if 2n + 1 points are placed in the grid, then by the pigeonhole principle some row and some column will contain three points. The problem was introduced by Henry Dudeney in 1917.

W

In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. For example, 4 can be partitioned in five distinct ways:4 3 + 1 2 + 2 2 + 1 + 1 1 + 1 + 1 + 1

W

In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset.

W

In physics, chemistry and materials science, percolation refers to the movement and filtering of fluids through porous materials. It is described by Darcy's law. Broader applications have since been developed that cover connectivity of many systems modeled as lattices or graphs, analogous to connectivity of lattice components in the filtration problem that modulates capacity for percolation.

W

In mathematics, the pigeonhole principle states that if items are put into containers, with , then at least one container must contain more than one item. For example, if you have three gloves, then you must have at least two right-hand gloves, or at least two left-hand gloves, because you have three objects, but only two categories of handedness to put them into. This seemingly obvious statement, a type of counting argument, can be used to demonstrate possibly unexpected results. For example, if you know that the population of London is greater than the maximum number of hairs that can be present on a human's head, then the pigeonhole principle requires that there must be at least two people in London who have the same number of hairs on their heads.

W

In mathematics, particularly in the fields of number theory and combinatorics, the rank of a partition of a positive integer is a certain integer associated with the partition. In fact at least two different definitions of rank appear in the literature. The first definition, with which most of this article is concerned, is that the rank of a partition is the number obtained by subtracting the number of parts in the partition from the largest part in the partition. The concept was introduced by Freeman Dyson in a paper published in the journal Eureka. It was presented in the context of a study of certain congruence properties of the partition function discovered by the Indian mathematical genius Srinivasa Ramanujan. A different concept, sharing the same name, is used in combinatorics, where the rank is taken to be the size of the Durfee square of the partition.

W

In combinatorics, the rule of product or multiplication principle is a basic counting principle. Stated simply, it is the idea that if there are a ways of doing something and b ways of doing another thing, then there are a · b ways of performing both actions.

W

Sequential dynamical systems (SDSs) are a class of graph dynamical systems. They are discrete dynamical systems which generalize many aspects of for example classical cellular automata, and they provide a framework for studying asynchronous processes over graphs. The analysis of SDSs uses techniques from combinatorics, abstract algebra, graph theory, dynamical systems and probability theory.

W

Sicherman dice are the only pair of 6-sided dice that are not normal dice, bear only positive integers, and have the same probability distribution for the sum as normal dice.

W

Sim is a pencil-and-paper game that is played by two players.

W

The Star of David theorem is a mathematical result on arithmetic properties of binomial coefficients. It was discovered by Henry W. Gould in 1972.

W

In combinatorial mathematics, a Stirling permutation of order k is a permutation of the multiset 1, 1, 2, 2, ..., k, k with the additional property that, for each value i appearing in the permutation, the values between the two copies of i are larger than i. For instance, the 15 Stirling permutations of order three are1,1,2,2,3,3; 1,2,2,1,3,3; 2,2,1,1,3,3; 1,1,2,3,3,2; 1,2,2,3,3,1; 2,2,1,3,3,1; 1,1,3,3,2,2; 1,2,3,3,2,1; 2,2,3,3,1,1; 1,3,3,1,2,2; 1,3,3,2,2,1; 2,3,3,2,1,1; 3,3,1,1,2,2; 3,3,1,2,2,1; 3,3,2,2,1,1.

W

In mathematics, a sunflower or -system is a collection of sets whose pairwise intersection is constant. This constant intersection is called the kernel of the sunflower.

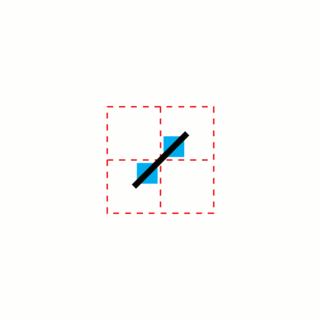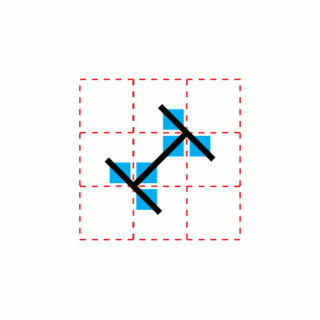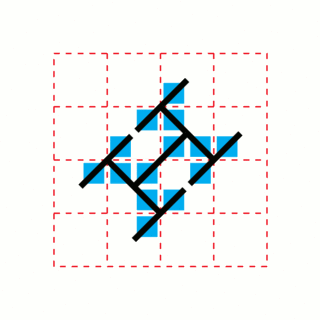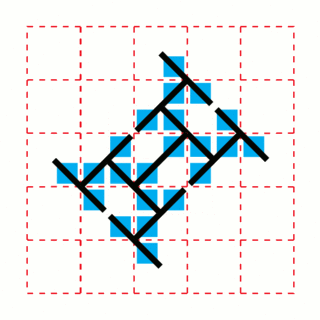W

In geometry, the toothpick sequence is a sequence of 2-dimensional patterns which can be formed by repeatedly adding line segments ("toothpicks") to the previous pattern in the sequence.

W

In mathematical combinatorics, the Transylvanian lottery is a lottery where three numbers between 1 and 14 are picked by the player for any given ticket, and three numbers are chosen randomly. The player wins if two of their numbers, on a given ticket, are among the random ones. The problem of how many tickets the player must buy in order to be certain of winning can be solved by the use of the Fano plane. (Mazur 2010, p.280 problem 15) (Javier Martínez, Gloria Gutiérrez & Pablo Cordero et al. 2008, p.85)

W

In mathematics, Tucker's lemma is a combinatorial analog of the Borsuk–Ulam theorem, named after Albert W. Tucker.