 W
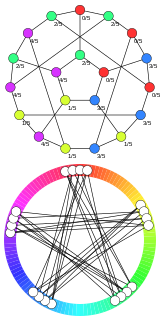
WIn graph theory, an Andrásfai graph is a triangle-free circulant graph named after Béla Andrásfai.
 W
WIn graph theory, a book graph may be any of several kinds of graph formed by multiple cycles sharing an edge.
 W
WIn mathematics, a bouquet graph , for an integer parameter , is an undirected graph with one vertex and edges, all of which are self-loops. It is the graph-theoretic analogue of the topological bouquet, a space of circles joined at a point. When the context of graph theory is clear, it can be called more simply a bouquet.
 W
WIn graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph , denoted can be given by any of the following definitions, all of which are equivalent. is the infimum over all real numbers so that there exists a map from to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance along this circle. is the infimum over all rational numbers so that there exists a map from to the cyclic group with the property that adjacent vertices map to elements at distance apart. In an oriented graph, declare the imbalance of a cycle to be divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, is the minimum imbalance of an orientation of .
 W
WThe Turán graph T(n,r) is a complete multipartite graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge if and only if they belong to different subsets. The graph will have subsets of size , and subsets of size . That is, it is a complete r-partite graph
 W
WIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.
 W
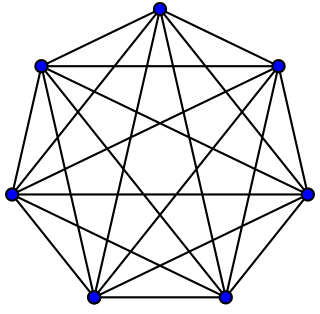
WIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.
 W
WIn graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by Preparata & Vuillemin (1981) for use as a network topology in parallel computing.
 W
WIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn. The number of vertices in Cn equals the number of edges, and every vertex has degree 2; that is, every vertex has exactly two edges incident with it.
 W
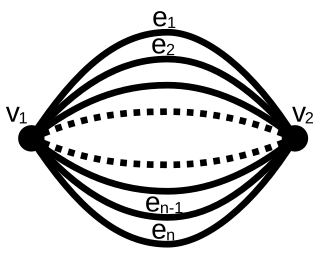
WIn graph theory, a dipole graph is a multigraph consisting of two vertices connected with a number of parallel edges. A dipole graph containing n edges is called the order-n dipole graph, and is denoted by Dn. The order-n dipole graph is dual to the cycle graph Cn.
 W
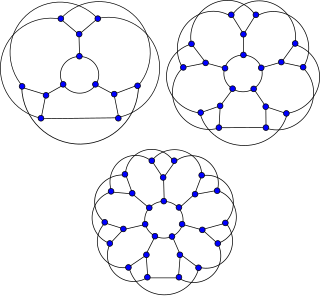
WIn the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.
 W
WIn graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.
 W
WIn graph theory and computational complexity theory, a Frankl–Rödl graph is a graph defined by connecting pairs of vertices of a hypercube that are at a specified even distance from each other. The graphs of this type are parameterized by the dimension of the hypercube and by the distance between adjacent vertices.
 W
WIn the mathematical field of graph theory, the friendship graph Fn is a planar undirected graph with 2n+1 vertices and 3n edges.
 W
WIn graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.
 W
WIn graph theory, a branch of mathematics, a half graph is a special type of bipartite graph. These graphs are called the half graphs because they have approximately half of the edges of a complete bipartite graph on the same vertices. The name was given to these graphs by Paul Erdős and András Hajnal.
 W
WIn graph theory, the halved cube graph or half cube graph of order n is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.
 W
WHamming graphs are a special class of graphs named after Richard Hamming and used in several branches of mathematics and computer science. Let S be a set of q elements and d a positive integer. The Hamming graph H(d,q) has vertex set Sd, the set of ordered d-tuples of elements of S, or sequences of length d from S. Two vertices are adjacent if they differ in precisely one coordinate; that is, if their Hamming distance is one. The Hamming graph H(d,q) is, equivalently, the Cartesian product of d complete graphs Kq.
 W
WIn graph theory and recreational mathematics, the Hanoi graphs are undirected graphs whose vertices represent the possible states of the Tower of Hanoi puzzle, and whose edges represent allowable moves between pairs of states.
 W
WIn graph theory, the hypercube graph Qn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cubical graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n−1n edges, and is a regular graph with n edges touching each vertex.
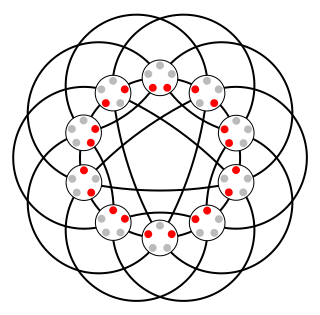 W
WJohnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph are the -element subsets of an -element set; two vertices are adjacent when the intersection of the two vertices (subsets) contains -elements. Both Johnson graphs and the closely related Johnson scheme are named after Selmer M. Johnson.
 W
WThe Kautz graph is a directed graph of degree and dimension , which has vertices labeled by all possible strings of length which are composed of characters chosen from an alphabet containing distinct symbols, subject to the condition that adjacent characters in the string cannot be equal.
 W
WIn geometry, Keller's conjecture is the conjecture that in any tiling of Euclidean space by identical hypercubes there are two cubes that meet face to face. For instance, as shown in the illustration, in any tiling of the plane by identical squares, some two squares must meet edge to edge.
 W
WIn graph theory, a king's graph is a graph that represents all legal moves of the king chess piece on a chessboard where each vertex represents a square on a chessboard and each edge is a legal move. More specifically, an king's graph is a king's graph of an chessboard. It is the map graph formed from the squares of a chessboard by making a vertex for each square and an edge for each two squares that share an edge or a corner. It can also be constructed as the strong product of two path graphs.
 W
WIn graph theory, the Kneser graph K(n, k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1955.
 W
WIn graph theory, a knight's graph, or a knight's tour graph, is a graph that represents all legal moves of the knight chess piece on a chessboard. Each vertex of this graph represents a square of the chessboard, and each edge connects two squares that are a knight's move apart from each other. More specifically, an knight's graph is a knight's graph of an chessboard. Its vertices can be represented as the points of the Euclidean plane whose Cartesian coordinates are integers with and , and with two vertices connected by an edge when their Euclidean distance is .
 W
WIn the mathematical field of graph theory, the ladder graph Ln is a planar undirected graph with 2n vertices and 3n-2 edges.
 W
WIn the mathematical discipline of graph theory, the (m,n)-lollipop graph is a special type of graph consisting of a complete graph (clique) on m vertices and a path graph on n vertices, connected with a bridge.
 W
WIn graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle. It is so-named because Mn has exactly n/2 4-cycles which link together by their shared edges to form a topological Möbius strip. Möbius ladders were named and first studied by Guy and Harary (1967).
 W
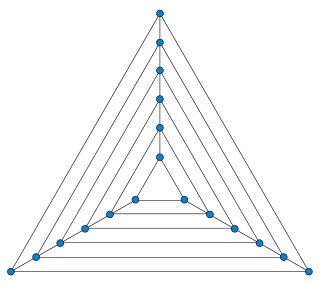
WIn graph theory, a nested triangles graph with n vertices is a planar graph formed from a sequence of n/3 triangles, by connecting pairs of corresponding vertices on consecutive triangles in the sequence. It can also be formed geometrically, by gluing together n/3 − 1 triangular prisms on their triangular faces. This graph, and graphs closely related to it, have been frequently used in graph drawing to prove lower bounds on the area requirements of various styles of drawings.
 W
WIn the mathematical field of graph theory, the odd graphs On are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.
 W
WIn mathematics, Paley graphs are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yield an infinite family of symmetric conference matrices. Paley graphs allow graph-theoretic tools to be applied to the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally.
 W
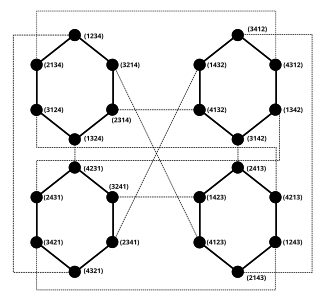
WIn the mathematical field of graph theory, the pancake graph Pn or n-pancake graph is a graph whose vertices are the permutations of n symbols from 1 to n and its edges are given between permutations transitive by prefix reversals.
 W
WIn graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge represents a legal move from one square to another. The same graphs can be defined mathematically as the Cartesian products of two complete graphs or as the line graphs of complete bipartite graphs.
 W
WIn graph theory, the shuffle-exchange network is an undirected cubic multigraph, whose vertices represent binary sequences of a given length and whose edges represent two operations on these sequence, circular shifts and flipping the lowest-order bit.
 W
WIn graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves. Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves.
 W
WIn the mathematics of Sudoku, the Sudoku graph is an undirected graph whose vertices represent the cells of a (blank) Sudoku puzzle and whose edges represent pairs of cells that belong to the same row, column, or block of the puzzle. The problem of solving a Sudoku puzzle can be represented as precoloring extension on this graph. It is an integral Cayley graph.
 W
WThe Turán graph T(n,r) is a complete multipartite graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge if and only if they belong to different subsets. The graph will have subsets of size , and subsets of size . That is, it is a complete r-partite graph
 W
WIn the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n-1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n+1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. In the rest of this article we use the former notation.
 W
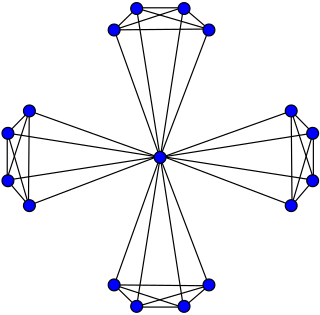
WIn the mathematical field of graph theory, the windmill graph Wd(k,n) is an undirected graph constructed for k ≥ 2 and n ≥ 2 by joining n copies of the complete graph Kk at a shared universal vertex. That is, it is a 1-clique-sum of these complete graphs.