40 Water waves

In fluid dynamics, wind waves, or wind-generated waves, are water surface waves that occur on the free surface of bodies of water. They result from the wind blowing over an area of fluid surface. Waves in the oceans can travel thousands of miles before reaching land. Wind waves on Earth range in size from small ripples, to waves over 100 ft (30 m) high, being limited by wind speed, duration, affected area and water depth.

In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell of the wave of translation. The 1872 paper of Boussinesq introduces the equations now known as the Boussinesq equations.

A bow wave is the wave that forms at the bow of a ship when it moves through the water. As the bow wave spreads out, it defines the outer limits of a ship's wake. A large bow wave slows the ship down, is a risk to smaller boats, and in a harbor can damage shore facilities and moored ships. Therefore, ship hulls are generally designed to produce as small a bow wave as possible.

In fluid dynamics, a breaking wave or breaker is a wave whose amplitude reaches a critical level at which some process can suddenly start to occur that causes large amounts of wave energy to be transformed into turbulent kinetic energy. At this point, simple physical models that describe wave dynamics often become invalid, particularly those that assume linear behaviour.

A capillary wave is a wave traveling along the phase boundary of a fluid, whose dynamics and phase velocity are dominated by the effects of surface tension.

In hydrodynamics, a clapotis is a non-breaking standing wave pattern, caused for example, by the reflection of a traveling surface wave train from a near vertical shoreline like a breakwater, seawall or steep cliff. The resulting clapotic wave does not travel horizontally, but has a fixed pattern of nodes and antinodes. These waves promote erosion at the toe of the wall, and can cause severe damage to shore structures. The term was coined in 1877 by French mathematician and physicist Joseph Valentin Boussinesq who called these waves 'le clapotis' meaning "the lapping".

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.

A cross sea is a sea state of wind-generated ocean waves that form nonparallel wave systems. Cross seas have a large amount of directional spreading. This may occur when water waves from one weather system continue despite a shift in wind. Waves generated by the new wind run at an angle to the old.

The Draupner wave or New Year's wave was the first rogue wave to be detected by a measuring instrument, occurring at the Draupner platform in the North Sea off the coast of Norway on 1 January 1995. In an area with significant wave height of approximately 12 metres (39 ft), a freak wave with a maximum wave height of 25.6 metres (84 ft) occurred. Prior to that measurement, no instrument-recorded evidence for rogue waves existed – only anecdotal evidence provided by those who had encountered them at sea, although ships such as the British weather ship Weather Reporter had recorded very large waves that did not differ quite enough from their neighbors to be considered rogue.

In fluid dynamics, an edge wave is a surface gravity wave fixed by refraction against a rigid boundary, often a shoaling beach. Progressive edge waves travel along this boundary, varying sinusoidally along it and diminishing exponentially in the offshore direction.

In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales or a transfer of energy from the small scales to the large scales. This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale, evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain.

Jannette Behrndtz Frandsen is a researcher and consultant who works in many fields including nearshore hydrodynamics, aeroelasticity, numerical analysis, computational fluid dynamics, coastal modeling, experimental fluid mechanics, sloshing, coastal erosion, climate change related problems, e.g., sea level rise, natural hazards, wind energy, biomimetics, wave energy.

In fluid dynamics, Green's law, named for 19th-century British mathematician George Green, is a conservation law describing the evolution of non-breaking, surface gravity waves propagating in shallow water of gradually varying depth and width. In its simplest form, for wavefronts and depth contours parallel to each other, it states: or

Infragravity waves are surface gravity waves with frequencies lower than the wind waves – consisting of both wind sea and swell – thus corresponding with the part of the wave spectrum lower than the frequencies directly generated by forcing through the wind.

Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.

In fluid dynamics, the Keulegan–Carpenter number, also called the period number, is a dimensionless quantity describing the relative importance of the drag forces over inertia forces for bluff objects in an oscillatory fluid flow. Or similarly, for objects that oscillate in a fluid at rest. For small Keulegan–Carpenter number inertia dominates, while for large numbers the (turbulence) drag forces are important.

This list of rogue waves compiles incidents of known and likely rogue waves – also known as freak waves, monster waves, killer waves, and extreme waves. These are dangerous and rare ocean surface waves that unexpectedly reach at least twice the height of the tallest waves around them, and are often described by witnesses as "walls of water". They occur in deep water, usually far out at sea, and are a threat even to capital ships and ocean liners.

A megatsunami is a very large wave created by a large, sudden displacement of material into a body of water.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.

The Peregrine soliton is an analytic solution of the nonlinear Schrödinger equation. This solution was proposed in 1983 by Howell Peregrine, researcher at the mathematics department of the University of Bristol.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.

Rogue waves are unusually large, unexpected and suddenly appearing surface waves that can be extremely dangerous, even to large ships such as ocean liners.

A seiche is a standing wave in an enclosed or partially enclosed body of water. Seiches and seiche-related phenomena have been observed on lakes, reservoirs, swimming pools, bays, harbours and seas. The key requirement for formation of a seiche is that the body of water be at least partially bounded, allowing the formation of the standing wave.

The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.

For a pure wave motion in fluid dynamics, the Stokes drift velocity is the average velocity when following a specific fluid parcel as it travels with the fluid flow. For instance, a particle floating at the free surface of water waves, experiences a net Stokes drift velocity in the direction of wave propagation.

In fluid dynamics, a Stokes wave is a nonlinear and periodic surface wave on an inviscid fluid layer of constant mean depth. This type of modelling has its origins in the mid 19th century when Sir George Stokes – using a perturbation series approach, now known as the Stokes expansion – obtained approximate solutions for nonlinear wave motion.

A storm surge, storm flood, tidal surge, or storm tide is a coastal flood or tsunami-like phenomenon of rising water commonly associated with low-pressure weather systems, such as cyclones. It is measured as the rise in water level above the normal tidal level, and does not include waves. Most casualties during tropical cyclones occur as the result of storm surges.

A surf break is a permanent obstruction such as a coral reef, rock, shoal, or headland that causes a wave to break, forming a barreling wave or other wave that can be surfed, before it eventually collapses. The topography of the seabed determines the shape of the wave and type of break. Since shoals can change size and location, affecting the break, it takes commitment and skill to find good breaks. Some surf breaks are quite dangerous, since the surfer can collide with a reef or rocks below the water.

A swell, in the context of an ocean, sea or lake, is a series of mechanical waves that propagate along the interface between water and air and thus are often referred to as surface gravity waves. These surface gravity waves are not wind waves, which are generated by the immediate local wind, but instead are generated by distant weather systems, where wind blows for a duration of time over a fetch of water. More generally, a swell consists of wind-generated waves that are not—or are hardly—affected by the local wind at that time. Swell waves often have a long wavelength, but this varies due to the size, strength, and duration of the weather system responsible for the swell and the size of the water body. Swell wavelength also varies from event to event. Occasionally, swells that are longer than 700m occur as a result of the most severe storms. Swell direction is the line or course on which the swell is moving. It is measured in degrees, and often referred to in general directions from which it is coming, such as an NNW or SW swell. Swells have a narrower range of frequencies and directions than locally generated wind waves, because they have dispersed from their generation area and dissipated. Swells take on a more defined shape and direction and are less random than locally generated wind waves.

In fluid dynamics, a trochoidal wave or Gerstner wave is an exact solution of the Euler equations for periodic surface gravity waves. It describes a progressive wave of permanent form on the surface of an incompressible fluid of infinite depth. The free surface of this wave solution is an inverted (upside-down) trochoid – with sharper crests and flat troughs. This wave solution was discovered by Gerstner in 1802, and rediscovered independently by Rankine in 1863.

In fluid dynamics, the Ursell number indicates the nonlinearity of long surface gravity waves on a fluid layer. This dimensionless parameter is named after Fritz Ursell, who discussed its significance in 1953.

In fluid dynamics, a wake may either be:the region of recirculating flow immediately behind a moving or stationary blunt body, caused by viscosity, which may be accompanied by flow separation and turbulence, or the wave pattern on the water surface downstream of an object in a flow, or produced by a moving object, caused by density differences of the fluids above and below the free surface and gravity.

The wave base, in physical oceanography, is the maximum depth at which a water wave's passage causes significant water motion. At water depths deeper than the wave base, bottom sediments and the seafloor are no longer stirred by the wave motion above.

In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering.

Wave radar is a type of radar for measuring wind waves. Several instruments based on a variety of different concepts and techniques are available, and these are all often called. This article, gives a brief description of the most common ground-based radar remote sensing techniques.

In fluid dynamics, wave shoaling is the effect by which surface waves entering shallower water change in wave height. It is caused by the fact that the group velocity, which is also the wave-energy transport velocity, changes with water depth. Under stationary conditions, a decrease in transport speed must be compensated by an increase in energy density in order to maintain a constant energy flux. Shoaling waves will also exhibit a reduction in wavelength while the frequency remains constant.

A wave tank is a laboratory setup for observing the behavior of surface waves. The typical wave tank is a box filled with liquid, usually water, leaving open or air-filled space on top. At one end of the tank an actuator generates waves; the other end usually has a wave-absorbing surface. A similar device is the ripple tank, which is flat and shallow and used for observing patterns of surface waves from above.

Wave-making resistance is a form of drag that affects surface watercraft, such as boats and ships, and reflects the energy required to push the water out of the way of the hull. This energy goes into creating the wave.

A wave-piercing boat hull has a very fine bow, with reduced buoyancy in the forward portions. When a wave is encountered, the lack of buoyancy means the hull pierces through the water rather than riding over the top, resulting in a smoother ride than traditional designs, and in diminished mechanical stress on the vessel. It also reduces a boat's wave-making resistance.

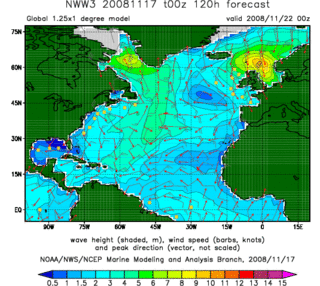
In fluid dynamics, wind wave modeling describes the effort to depict the sea state and predict the evolution of the energy of wind waves using numerical techniques. These simulations consider atmospheric wind forcing, nonlinear wave interactions, and frictional dissipation, and they output statistics describing wave heights, periods, and propagation directions for regional seas or global oceans. Such wave hindcasts and wave forecasts are extremely important for commercial interests on the high seas. For example, the shipping industry requires guidance for operational planning and tactical seakeeping purposes.