 W
WIn graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
 W
WIn graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is an edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.
 W
WIn graph theory, an acyclic coloring is a (proper) vertex coloring in which every 2-chromatic subgraph is acyclic. The acyclic chromatic number A(G) of a graph G is the fewest colors needed in any acyclic coloring of G.
 W
WIn graph theory, a total coloring is a coloring on the vertices and edges of a graph such that:
 W
WIn combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of his many conjectures in graph coloring theory. The conjecture states that, among all graphs requiring colors, the complete graph is the one with the smallest crossing number. Equivalently, if a graph can be drawn with fewer crossings than , then, according to the conjecture, it may be colored with fewer than colors.
 W
WIn graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a connected graph in which every vertex has at most Δ neighbors, the vertices can be colored with only Δ colors, except for two cases, complete graphs and cycle graphs of odd length, which require Δ + 1 colors.
 W
WIn the mathematics of graph coloring, Cereceda’s conjecture is an unsolved problem on the distance between pairs of colorings of sparse graphs. It states that, for two different colorings of a graph of degeneracy d, both using at most d + 2 colors, it should be possible to reconfigure one coloring into the other by changing the color of one vertex at a time, using a number of steps that is quadratic in the size of the graph. The conjecture is named after Luis Cereceda, who formulated it in his 2007 doctoral dissertation.
 W
WThe chromatic polynomial is a graph polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to study the four color problem. It was generalised to the Tutte polynomial by Hassler Whitney and W. T. Tutte, linking it to the Potts model of statistical physics.
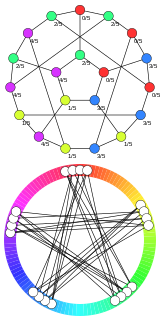 W
WIn graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph , denoted can be given by any of the following definitions, all of which are equivalent. is the infimum over all real numbers so that there exists a map from to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance along this circle. is the infimum over all rational numbers so that there exists a map from to the cyclic group with the property that adjacent vertices map to elements at distance apart. In an oriented graph, declare the imbalance of a cycle to be divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, is the minimum imbalance of an orientation of .
 W
WIn graph theory, a cocoloring of a graph G is an assignment of colors to the vertices such that each color class forms an independent set in G or in the complement of G. The cochromatic number z(G) of G is the fewest colors needed in any cocolorings of G. The graphs with cochromatic number 2 are exactly the bipartite graphs, complements of bipartite graphs, and split graphs.
 W
WIn graph theory, complete coloring is the opposite of harmonious coloring in the sense that it is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic number ψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.
 W
WIn graph theory, a critical graph is a graph G in which every vertex or edge is a critical element, that is, if its deletion decreases the chromatic number of G. Such a decrease cannot be by more than 1.
 W
WIn graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that destroys all of the nontrivial symmetries of the graph. The coloring does not need to be a proper coloring: adjacent vertices are allowed to be given the same color. For the colored graph, there should not exist any one-to-one mapping of the vertices to themselves that preserves both adjacency and coloring. The minimum number of colors in a distinguishing coloring is called the distinguishing number of the graph.
 W
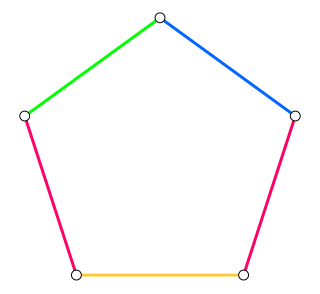
WIn graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
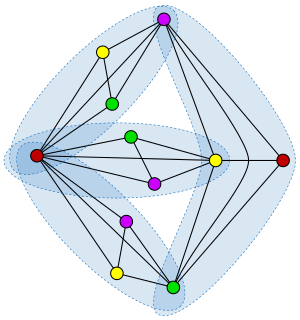 W
WIn graph theory, the Erdős–Faber–Lovász conjecture is an unsolved problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:If k complete graphs, each having exactly k vertices, have the property that every pair of complete graphs has at most one shared vertex, then the union of the graphs can be colored with k colors.
 W
WIn graph theory, an exact coloring is a (proper) vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. That is, it is a partition of the vertices of the graph into disjoint independent sets such that, for each pair of distinct independent sets in the partition, there is exactly one edge with endpoints in each set.
 W
WIn mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. Since then the proof has gained wide acceptance, although some doubters remain.
 W
WFractional coloring is a topic in a young branch of graph theory known as fractional graph theory. It is a generalization of ordinary graph coloring. In a traditional graph coloring, each vertex in a graph is assigned some color, and adjacent vertices — those connected by edges — must be assigned different colors. In a fractional coloring however, a set of colors is assigned to each vertex of a graph. The requirement about adjacent vertices still holds, so if two vertices are joined by an edge, they must have no colors in common.
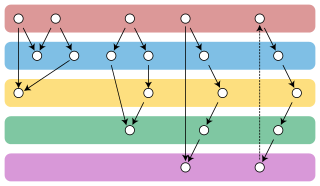 W
WIn graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph G equals one plus the length of a longest path in an orientation of G chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.
 W
WIn the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not in general use the minimum number of colors possible.
 W
WIn the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors. According to the four-color theorem, every graph that can be drawn in the plane without edge crossings can have its vertices colored using at most four different colors, so that the two endpoints of every edge have different colors, but according to Grötzsch's theorem only three colors are needed for planar graphs that do not contain three mutually-adjacent vertices.
 W
WIn graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939. The undirected version was introduced by Christen & Selkow (1979).
 W
WIn graph theory, the Hadwiger conjecture states that if G is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
 W
WIn geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.
 W
WIn graph theory, a harmonious coloring is a (proper) vertex coloring in which every pair of colors appears on at most one pair of adjacent vertices. The harmonious chromatic number χH(G) of a graph G is the minimum number of colors needed for any harmonious coloring of G.
 W
WIn mathematics, the Heawood number of a surface is a certain upper bound for the maximal number of colors needed to color any graph embedded in the surface.
 W
WIn graph theory, Hedetniemi's conjecture, formulated by Stephen T. Hedetniemi in 1966, concerns the connection between graph coloring and the tensor product of graphs. This conjecture states that
 W
WIn mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of points on a graph with alternating colors.
 W
WL(2, 1)-coloring is a particular case of L(h, k)-coloring which is in fact a proper coloring. In L(2, 1)-coloring of a graph, G, the vertices of the graph G is colored or labelled in such a way that the adjacent vertices get labels that differ by at least two. Also the vertices that are at a distance of two from each other get labels that differ by at least one.
 W
WIn graph theory and theoretical computer science, the monochromatic triangle problem is an algorithmic problem on graphs, in which the goal is to partition the edges of a given graph into two triangle-free subgraphs. It is NP-complete but fixed-parameter tractable on graphs of bounded treewidth.
 W
WIn graph theory, a branch of mathematics, a radio coloring of an undirected graph is a form of graph coloring in which one assigns positive integer labels to the graphs such that the labels of adjacent vertices differ by at least two, and the labels of vertices at distance two from each other differ by at least one. Radio coloring was first studied by Griggs & Yeh (1992), under a different name, L(2,1)-labeling. It was called radio coloring by Frank Harary because it models the problem of channel assignment in radio broadcasting, while avoiding electromagnetic interference between radio stations that are near each other both in the graph and in their assigned channel frequencies.
 W
WIn graph theory, a path in an edge-colored graph is said to be rainbow if no color repeats on it. A graph is said to be rainbow-connected if there is a rainbow path between each pair of its vertices. If there is a rainbow shortest path between each pair of vertices, the graph is said to be strongly rainbow-connected.
 W
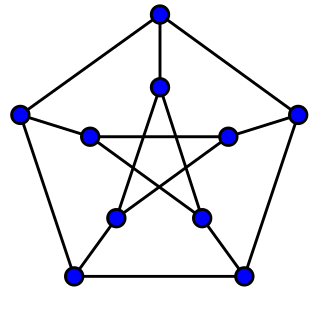
WIn the mathematical field of graph theory, a snark is a simple, connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, the connectivity is redundant so that removing no one edge would split the graph, and the edges cannot be colored by only three colors without two edges of the same color meeting at a point. In order to avoid trivial cases, snarks are often restricted to have girth at least 5.
 W
WIn graph-theoretic mathematics, a star coloring of a graph G is a (proper) vertex coloring in which every path on four vertices uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected components that are star graphs. Star coloring has been introduced by Grünbaum (1973). The star chromatic number of G is the fewest colors needed to star color G.
 W
WIn graph theory, a strong coloring, with respect to a partition of the vertices into (disjoint) subsets of equal sizes, is a (proper) vertex coloring in which every color appears exactly once in every part. A graph is strongly k-colorable if, for each partition of the vertices into sets of size k, it admits a strong coloring. When the order of the graph G is not divisible by k, we add isolated vertices to G just enough to make the order of the new graph G′ divisible by k. In that case, a strong coloring of G′ minus the previously added isolated vertices is considered a strong coloring of G.
 W
WIn graph theory, a subcoloring is an assignment of colors to a graph's vertices such that each color class induces a vertex disjoint union of cliques. That is, each color class should form a cluster graph.
 W
WIn graph theory, a sum coloring of a graph is a labeling of its vertices by positive integers, with no two adjacent vertices having equal labels, that minimizes the sum of the labels. The minimum sum that can be achieved is called the chromatic sum of the graph. Chromatic sums and sum coloring were introduced by Supowit in 1987 using non-graph-theoretic terminology, and first studied in graph theoretic terms by Ewa Kubicka in her 1989 doctoral thesis.
 W
WIn graph theory, a T-Coloring of a graph , given the set T of nonnegative integers containing 0, is a function that maps each vertex to a positive integer (color) such that if u and w are adjacent then . In simple words, the absolute value of the difference between two colors of adjacent vertices must not belong to fixed set T. The concept was introduced by William K. Hale. If T = {0} it reduces to common vertex coloring.
 W
WIn the mathematical area of graph theory, the Thue number of a graph is a variation of the chromatic index, defined by Alon et al. (2002) and named after mathematician Axel Thue, who studied the squarefree words used to define this number.
 W
WIn graph theory, total coloring is a type of graph coloring on the vertices and edges of a graph. When used without any qualification, a total coloring is always assumed to be proper in the sense that no adjacent edges and no edge and its endvertices are assigned the same color. The total chromatic number χ″(G) of a graph G is the fewest colors needed in any total coloring of G.
 W
WIn the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non-isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial.
 W
WIn graph theory, a subfield of mathematics, a well-colored graph is an undirected graph for which greedy coloring uses the same number of colors regardless of the order in which colors are chosen for its vertices. That is, for these graphs, the chromatic number and Grundy number are equal.