45 Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice-versa.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

An (simple) arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of curved figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called k-arcs. An important generalization of the k-arc concept, also referred to as arcs in the literature, are the -arcs.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.

In mathematics, a Cayley–Klein metric is a metric on the complement of a fixed quadric in a projective space which is defined using a cross-ratio. The construction originated with Arthur Cayley's essay "On the theory of distance" where he calls the quadric the absolute. The construction was developed in further detail by Felix Klein in papers in 1871 and 1873, and subsequent books and papers. The Cayley–Klein metrics are a unifying idea in geometry since the method is used to provide metrics in hyperbolic geometry, elliptic geometry, and Euclidean geometry. The field of non-Euclidean geometry rests largely on the footing provided by Cayley–Klein metrics.

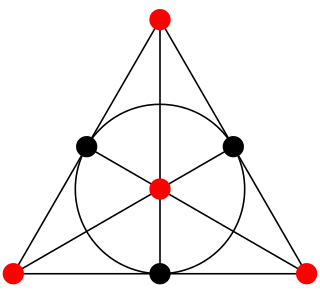
In mathematics, specifically in incidence geometry and especially in projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in a plane, no three of which are on a common line, and of the six lines connecting the six pairs of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.

In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines through the origin of a complex Euclidean space. Formally, a complex projective space is the space of complex lines through the origin of an (n+1)-dimensional complex vector space. The space is denoted variously as P(Cn+1), Pn(C) or CPn. When n = 1, the complex projective space CP1 is the Riemann sphere, and when n = 2, CP2 is the complex projective plane.

In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points A, B, C and D on a line, their cross ratio is defined as

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect in one and only one point.

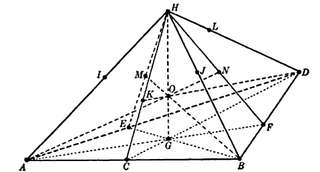
In projective geometry, a desmic system is a set of three tetrahedra in 3-dimensional projective space, such that any two are desmic,. It was introduced by Stephanos (1879). The three tetrahedra of a desmic system are contained in a pencil of quartic surfaces. The name "desmic" comes from the Greek word δεσμός, meaning band or chain, referring to the pencil of quartics.

In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree of the dual is known as the class of the original curve. The equation of the dual of C, given in line coordinates, is known as the tangential equation of C.

In finite geometry, the Fano plane is the finite projective plane of order 2. It is the finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2) where PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

A gnomonic map projection displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees.

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.

In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined.

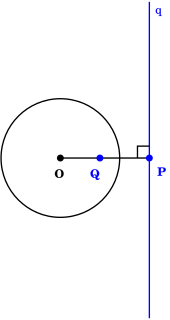
In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.

A Lénárt sphere is a teaching and educational research model for spherical geometry. The Lénárt sphere is a modern replacement of a "spherical blackboard". It can be used for visualizing spherical polygons showing the relationships between the sides and the angles.

In geometry, the nine-point conic of a complete quadrangle is a conic that passes through the three diagonal points and the six midpoints of sides of the complete quadrangle.

In projective geometry an oval is a circle-like pointset (curve) in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension d ≥ 3. Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid are:Any line intersects in at most 2 points, The tangents at a point cover a hyperplane, and contains no lines.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.

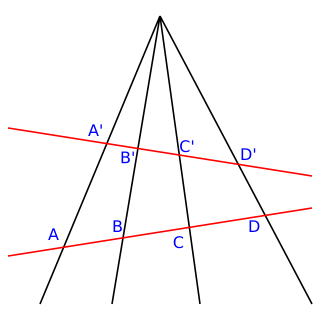
Two figures in a plane are perspective from a point O if the lines joining corresponding points of the figures all meet at O. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions.

In finite geometry, PG(3,2) is the smallest three-dimensional projective space. It can be thought of as an extension of the Fano plane. It has 15 points, 35 lines, and 15 planes. It also has the following properties:Each point is contained in 7 lines and 7 planes Each line is contained in 3 planes and contains 3 points Each plane contains 7 points and 7 lines Each plane is isomorphic to the Fano plane Every pair of distinct planes intersect in a line A line and a plane not containing the line intersect in exactly one point

In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.

In geometry, the pole and polar are respectively a point and a line that have a unique reciprocal relationship with respect to a given conic section.

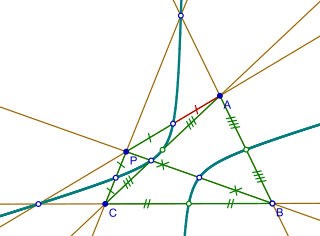
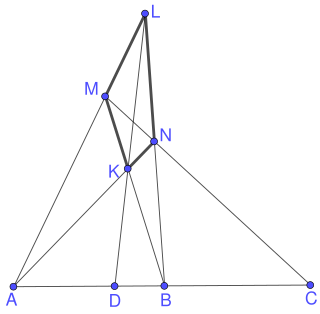
In projective geometry, the harmonic conjugate point of an ordered triple of points on the real projective line is defined by the following construction:Given three collinear points A, B, C, let L be a point not lying on their join and let any line through C meet LA, LB at M, N respectively. If AN and BM meet at K, and LK meets AB at D, then D is called the harmonic conjugate of C with respect to A, B.

In mathematics, the projective line over a ring is an extension of the concept of projective line over a field. Given a ring A with 1, the projective line P(A) over A consists of points identified by projective coordinates. Let U be the group of units of A; pairs and from A × A are related when there is a u in U such that ua = c and ub = d. This relation is an equivalence relation. A typical equivalence class is written U[a, b].

In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient groupPGL(V) = GL(V)/Z(V)

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .

In real analysis, the projectively extended real line, is the extension of the set of the real numbers, by a point denoted ∞. It is thus the set with the standard arithmetic operations extended where possible, and is sometimes denoted by The added point is called the point at infinity, because it is considered as a neighbour of both ends of the real line. More precisely, the point at infinity is the limit of every sequence of real numbers whose absolute values are increasing and unbounded.

In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface

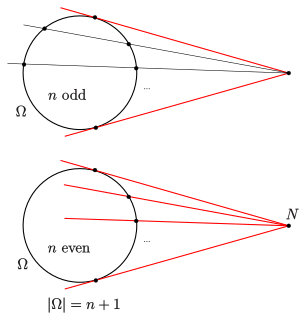
In projective geometry Qvist's theorem, named after the Finnish mathematician Bertil Qvist, is a statement on ovals in finite projective planes. Standard examples of ovals are non-degenerate (projective) conic sections. The theorem gives an answer to the question How many tangents to an oval can pass through a point in a finite projective plane? The answer depends essentially upon the order of the plane.

In geometry, a real projective line is an extension of the usual concept of line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity". For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line. It is the circle of directions emanating from an observer situated at any point, with opposite points identified. A model of the real projective line is the projectively extended real line. Drawing a line to represent the horizon in visual perspective, an additional point at infinity is added to represent the collection of lines parallel to the horizon.

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane, the complex plane plus a point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value ∞ for infinity. With the Riemann model, the point "∞" is near to very large numbers, just as the point "0" is near to very small numbers.

In geometry, a Schlegel diagram is a projection of a polytope from into through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in that, together with the original facet, is combinatorially equivalent to the original polytope. The diagram is named for Victor Schlegel, who in 1886 introduced this tool for studying combinatorial and topological properties of polytopes. In dimension 3, a Schlegel diagram is a projection of a polyhedron into a plane figure; in dimension 4, it is a projection of a 4-polytope to 3-space. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes.

In projective geometry, Segre's theorem, named after the Italian mathematician Beniamino Segre, is the statement:Any oval in a finite pappian projective plane of odd order is a nondegenerate projective conic section.

In mathematics, the special linear group SL(2,R) or SL2(R) is the group of 2 × 2 real matrices with determinant one:

In projective geometry, a special conformal transformation is a linear fractional transformation that is not an affine transformation. Thus the generation of a special conformal transformation involves use of multiplicative inversion, which is the generator of linear fractional transformations that is not affine.

In geometry, the stereographic projection is a particular mapping (function) that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point: the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it preserves angles at which curves meet. It is neither isometric nor area-preserving: that is, it preserves neither distances nor the areas of figures.

In tropical geometry, a tropical projective space is the tropical analog of the classic projective space.

A visual hull is a geometric entity created by shape-from-silhouette 3D reconstruction technique introduced by A. Laurentini. This technique assumes the foreground object in an image can be separated from the background. Under this assumption, the original image can be thresholded into a foreground/background binary image, which we call a silhouette image. The foreground mask, known as a silhouette, is the 2D projection of the corresponding 3D foreground object. Along with the camera viewing parameters, the silhouette defines a back-projected generalized cone that contains the actual object. This cone is called a silhouette cone. The upper right thumbnail shows two such cones produced from two silhouette images taken from different viewpoints. The intersection of the two cones is called a visual hull, which is a bounding geometry of the actual 3D object.

In geometry, a W-curve is a curve in projective n-space that is invariant under a 1-parameter group of projective transformations. W-curves were first investigated by Felix Klein and Sophus Lie in 1871, who also named them. W-curves in the real projective plane can be constructed with straightedge alone. Many well-known curves are W-curves, among them conics, logarithmic spirals, powers (like y = x3), logarithms and the helix, but not e.g. the sine. W-curves occur widely in the realm of plants.