48 Functions and mappings

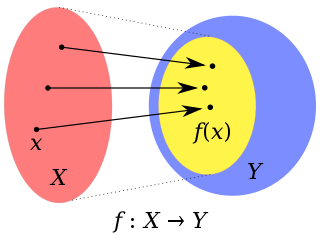
In mathematics, a function is a binary relation between two sets that associates every element of the first set to exactly one element of the second set. Typical examples are functions from integers to integers, or from the real numbers to real numbers.

In mathematics, a map is often used as a synonym for a function, but may also refer to some generalizations. Originally, this was an abbreviation of mapping, which often refers to the action of applying a function to the elements of its domain. This terminology is not completely fixed, as these terms are generally not formally defined, and can be considered to be jargon. These terms may have originated as a generalization of the process of making a geographical map, which consists of mapping the Earth surface to a sheet of paper.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

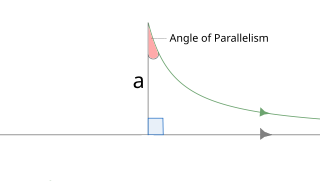
In hyperbolic geometry, the angle of parallelism , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.

A bell-shaped function or simply 'bell curve' is a mathematical function having a characteristic "bell"-shaped curve. These functions are typically continuous or smooth, asymptotically approach zero for large negative/positive x, and have a single, unimodal maximum at small x. Hence, the integral of a bell-shaped function is typically a sigmoid function. Bell shaped functions are also commonly symmetric.

In the mathematical theory of functions of one or more complex variables, and also in complex algebraic geometry, a biholomorphism or biholomorphic function is a bijective holomorphic function whose inverse is also holomorphic.

In mathematics, a bijection, bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function f: X → Y is a one-to-one (injective) and onto (surjective) mapping of a set X to a set Y. The term one-to-one correspondence must not be confused with one-to-one function.

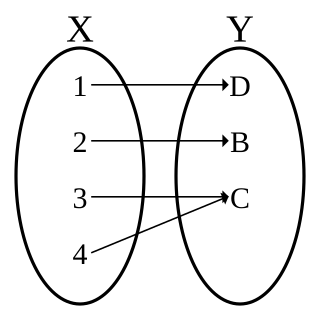
In mathematics, injections, surjections and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.

In number theory, a branch of mathematics, the Carmichael function associates to every positive integer n a positive integer λ(n), defined as the smallest positive integer m such thatam ≡ 1

In mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set Y in the notation f: X → Y. The term range is sometimes ambiguously used to refer to either the codomain or image of a function.

The Crystal Ball function, named after the Crystal Ball Collaboration, is a probability density function commonly used to model various lossy processes in high-energy physics. It consists of a Gaussian core portion and a power-law low-end tail, below a certain threshold. The function itself and its first derivative are both continuous.

In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value with respect to a change in its argument. Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.

In mathematics, the domain or set of departure of a function is the set into which all of the input of the function is constrained to fall. It is the set X in the notation f: X → Y, and is alternatively denoted as . Since a function is defined on its entire domain, its domain coincides with its domain of definition. However, this coincidence is no longer true for a partial function, since the domain of definition of a partial function can be a proper subset of the domain.

In mathematics, a geometric transformation is any bijection of a set to itself with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both or both — such that the function is injective so that its inverse exists. The study of geometry may be approached via the study of these transformations.

In 2-dimensional geometry, a glide reflection is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation. The intermediate step between reflection and translation can look different from the starting configuration, so objects with glide symmetry are in general, not symmetrical under reflection alone. In group theory, the glide plane is classified as a type of opposite isometry of the Euclidean plane

In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane.

In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word homeomorphism comes from the Greek words ὅμοιος (homoios) = similar or same and μορφή (morphē) = shape, form, introduced to mathematics by Henri Poincaré in 1895.

In the field of computer vision, any two images of the same planar surface in space are related by a homography. This has many practical applications, such as image rectification, image registration, or computation of camera motion—rotation and translation—between two images. Once camera rotation and translation have been extracted from an estimated homography matrix, this information may be used for navigation, or to insert models of 3D objects into an image or video, so that they are rendered with the correct perspective and appear to have been part of the original scene.

In mathematics, an identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument. That is, for f being identity, the equality f(x) = x holds for all x.

In mathematics, if A is a subset of B, then the inclusion map is the function ι that sends each element x of A to x, treated as an element of B:

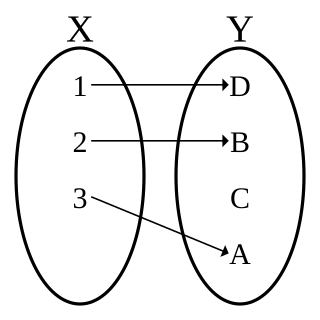
In mathematics, an injective function is a function that maps distinct elements of its domain to distinct elements of its codomain. In other words, every element of the function's codomain is the image of at most one element of its domain. The term one-to-one function must not be confused with one-to-one correspondence that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain.

In mathematics, an integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.

In mathematics, an involution, or an involutory function, is a function f that is its own inverse,f(f ) = x

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective.

In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain X to a codomain Y associates each x in X to one or more values y in Y; it is thus a serial binary relation. Some authors allow a multivalued function to have no value for some inputs.

In calculus, a one-sided limit is either of the two limits of a function f(x) of a real variable x as x approaches a specified point either from the left or from the right.

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much that sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits, there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real-valued function at a point, and oscillation of a function on an interval.

In signal processing, any periodic function, with period P, can be represented by a summation of an infinite number of instances of an aperiodic function, , that are offset by integer multiples of P. This representation is called periodic summation:

Linear or point-projection perspective is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight appear shorter than its dimensions across the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon line depending on the view used.

In mathematics, a piecewise-defined function is a function defined by multiple sub-functions, where each sub-function applies to a different interval in the domain. Piecewise is actually a way of expressing the function, rather than a characteristic of the function itself, but with additional qualification, it can describe the nature of the function.

The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group, which is of importance as a model in our understanding the most basic fundamentals of physics. For example, in one way of rigorously defining exactly what a subatomic particle is, Sheldon Lee Glashow has expressed that "Particles are at a very minimum described by irreducible representations of the Poincaré group."

In geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space. An object that is invariant under a point reflection is said to possess point symmetry; if it is invariant under point reflection through its center, it is said to possess central symmetry or to be centrally symmetric.

In mathematics, the range of a function may refer to either of two closely related concepts:The codomain of the function The image of the function

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state.

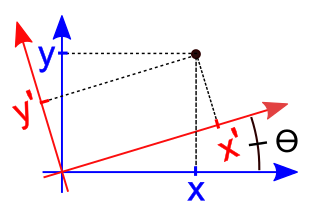
In mathematics, a rotation of axes in two dimensions is a mapping from an xy-Cartesian coordinate system to an x'y'-Cartesian coordinate system in which the origin is kept fixed and the x' and y' axes are obtained by rotating the x and y axes counterclockwise through an angle . A point P has coordinates with respect to the original system and coordinates with respect to the new system. In the new coordinate system, the point P will appear to have been rotated in the opposite direction, that is, clockwise through the angle . A rotation of axes in more than two dimensions is defined similarly. A rotation of axes is a linear map and a rigid transformation.

In calculus, the second derivative, or the second order derivative, of a function f is the derivative of the derivative of f. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of the object is changing with respect to time. In Leibniz notation:

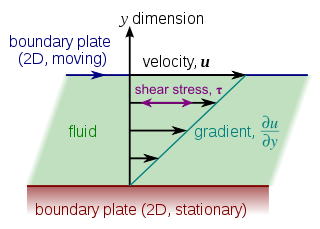
In plane geometry, a shear mapping is a linear map that displaces each point in a fixed direction, by an amount proportional to its signed distance from the line that is parallel to that direction and goes through the origin. This type of mapping is also called shear transformation, transvection, or just shearing.

Shekel function is a multidimensional, multimodal, continuous, deterministic function commonly used as a test function for testing optimization techniques.

In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a rotation or shear mapping.

In calculus, the squeeze theorem, also known as the pinching theorem, the sandwich theorem, the sandwich rule, the police theorem and sometimes the squeeze lemma, is a theorem regarding the limit of a function. In Italy, the theorem is also known as theorem of carabinieri.

Steiner's problem, asked and answered by Steiner (1850), is the problem of finding the maximum of the function

In mathematics, a function f from a set X to a set Y is surjective, if for every element y in the codomain Y of f, there is at least one element x in the domain X of f such that f(x) = y. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.

In mathematics, a transformation is a function f that maps a set X to itself, i.e. f : X → X. In other areas of mathematics, a transformation may simply refer to any function, regardless of domain and codomain. For this wider sense of the term, see function (mathematics).

In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure or a space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In a Euclidean space, any translation is an isometry.

The Upsilon function, Υ(s), is a function of a complex variable s that analytically continues the sum of the infinite series

The vector projection of a vector a on a nonzero vector b, sometimes denoted , is the orthogonal projection of a onto a straight line parallel to b. It is a vector parallel to b, defined as:

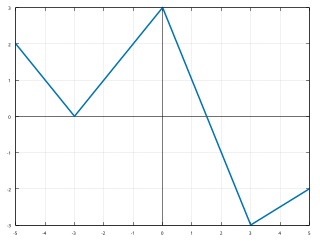
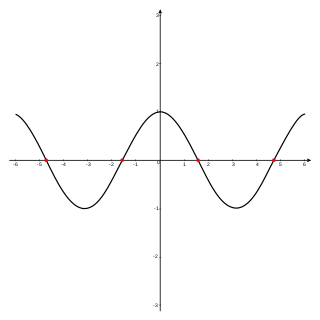
In mathematics, the vertical line test is a visual way to determine if a curve is a graph of a function or not. A function can only have one output, y, for each unique input, x. If a vertical line intersects a curve on an xy-plane more than once then for one value of x the curve has more than one value of y, and so, the curve does not represent a function. If all vertical lines intersect a curve at most once then the curve represents a function.

In mathematics, a zero of a real-, complex-, or generally vector-valued function , is a member of the domain of such that vanishes at ; that is, the function attains the value of 0 at , or equivalently, is the solution to the equation . A "zero" of a function is thus an input value that produces an output of .