 W
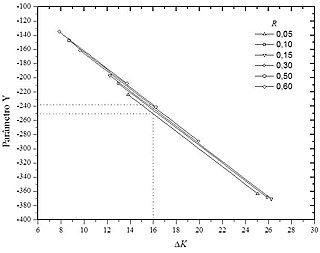
WThe alpha-beta model is a mathematical equation used to describe the velocity of fatigue crack growth, da / dN, as a function of a constant amplitude load driving force ΔK where its constants α and β are obtained through a semi-empirical process. Originally the alpha-beta model was developed and tested from data generated in tests using commercial grade Titanium and Aluminium Alloy 2524-T3 both the structural materials of great interest aeronautical. This model is applied in two situations: the individual that conforms to the experimental data of a single test and can be compared to Paris' law; and the generalized one that tries to represent in a bi-parametric way the effects of R - ratio between the tensions intensity, minimum and maximum - for a set of tests in the same material.
 W
WThe Avrami equation describes how solids transform from one phase to another at constant temperature. It can specifically describe the kinetics of crystallisation, can be applied generally to other changes of phase in materials, like chemical reaction rates, and can even be meaningful in analyses of ecological systems.
 W
WIn thermodynamics, Bridgman's thermodynamic equations are a basic set of thermodynamic equations, derived using a method of generating multiple thermodynamic identities involving a number of thermodynamic quantities. The equations are named after the American physicist Percy Williams Bridgman..
 W
WIn algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial
 W
WIn physics, the Callan–Symanzik equation is a differential equation describing the evolution of the n-point correlation functions under variation of the energy scale at which the theory is defined and involves the beta function of the theory and the anomalous dimensions.
 W
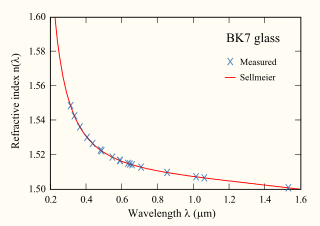
WIn optics, Cauchy's transmission equation is an empirical relationship between the refractive index and wavelength of light for a particular transparent material. It is named for the mathematician Augustin-Louis Cauchy, who defined it in 1836.
 W
WIn algebra, a cubic equation in one variable is an equation of the form
 W
WDilution is the process of decreasing the concentration of a solute in a solution, usually simply by mixing with more solvent like adding more water to the solution. To dilute a solution means to add more solvent without the addition of more solute. The resulting solution is thoroughly mixed so as to ensure that all parts of the solution are identical.
 W
WThe Drake equation is a probabilistic argument used to estimate the number of active, communicative extraterrestrial civilizations in the Milky Way galaxy.
 W
WDynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.
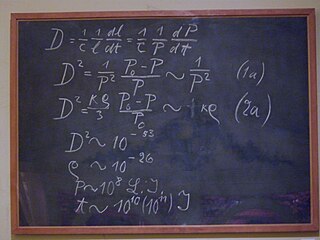 W
WEinstein's Blackboard is a blackboard which physicist Albert Einstein (1879–1955) used on 16 May 1931 during his lectures while visiting the University of Oxford in England. The blackboard is one of the most iconic objects in the collection of the Museum of the History of Science in Oxford.
 W
WThe equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconcile a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion. Apparent solar time can be obtained by measurement of the current position of the Sun, as indicated by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
 W
WIn mathematics, to solve an equation is to find its solutions, which are the values that fulfill the condition stated by the equation, consisting generally of two expressions related by an equals sign. When seeking a solution, one or more variables are designated as unknowns. A solution is an assignment of values to the unknown variables that makes the equality in the equation true. In other words, a solution is a value or a collection of values such that, when substituted for the unknowns, the equation becomes an equality. A solution of an equation is often called a root of the equation, particularly but not only for polynomial equations. The set of all solutions of an equation is its solution set.
 W
WEuler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam that are subjected to lateral loads only. It is thus a special case of Timoshenko beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
 W
WThe Fenske equation in continuous fractional distillation is an equation used for calculating the minimum number of theoretical plates required for the separation of a binary feed stream by a fractionation column that is being operated at total reflux.
 W
WIn statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, and is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered the concept in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation, and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is known in statistical mechanics as the Liouville equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion.
 W
WThe Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density and pressure . The equations for negative spatial curvature were given by Friedmann in 1924.
 W
WGravity, in the context of fermenting alcoholic beverages, refers to the specific gravity, or relative density compared to water, of the wort or must at various stages in the fermentation. The concept is used in the brewing and wine-making industries. Specific gravity is measured by a hydrometer, refractometer, pycnometer or oscillating U-tube electronic meter.
 W
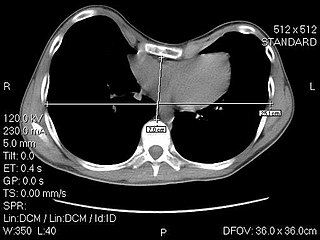
WThe Haller index, created in 1987 by J. Alex Haller, S. S. Kramer, and S. A. Lietman, is a mathematical relationship that exists in a human chest section observed with a CT scan. It is defined as the ratio of the transverse diameter and the anteroposterior diameter.
 W
WI = PAT is the mathematical notation of a formula put forward to describe the impact of human activity on the environment.I = P × A × T
 W
WIn astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:The orbit of a planet is an ellipse with the Sun at one of the two foci. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
 W
WThe Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
 W
WLamé's special quartic, named after Gabriel Lamé, is the graph of the equation
 W
WIn mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as
 W
WIn mathematics, a linear equation is an equation that may be put in the form
 W
WThe London equations, developed by brothers Fritz and Heinz London in 1935, are constitutive relations for a superconductor relating its superconducting current to electromagnetic fields in and around it. Whereas Ohm's law is the simplest constitutive relation for an ordinary conductor, the London equations are the simplest meaningful description of superconducting phenomena, and form the genesis of almost any modern introductory text on the subject. A major triumph of the equations is their ability to explain the Meissner effect, wherein a material exponentially expels all internal magnetic fields as it crosses the superconducting threshold.
 W
WIn physics, mass–energy equivalence is the relationship between mass and energy in a system’s rest frame, where the two values differ only by a constant and the units of measurement. The principle is described by Albert Einstein's famous formula:
 W
WIn physics, specifically general relativity, the Mathisson–Papapetrou–Dixon equations describe the motion of a massive spinning body moving in a gravitational field. Other equations with similar names and mathematical forms are the Mathisson–Papapetrou equations and Papapetrou–Dixon equations. All three sets of equations describe the same physics.
 W
WThe first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book Opticks. Prism pair expanders were introduced by Brewster in 1813. A modern mathematical description of the single-prism dispersion was given by Born and Wolf in 1959. The generalized multiple-prism dispersion theory was introduced by Duarte and Piper in 1982.
 W
WPappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.
 W
WIn mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization of the object.
 W
WIn mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:
 W
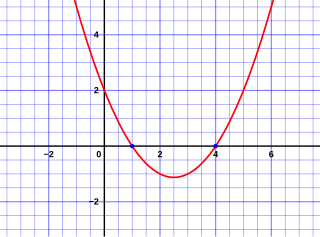
WIn elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring, completing the square, graphing and others.
 W
WIn mathematics, a quartic equation is one which can be expressed as a quartic function equalling zero. The general form of a quartic equation is
 W
WIn algebra, a quartic function is a function of the form
 W
WIn algebra, a quintic function is a function of the form
 W
WThe Rabinovich–Fabrikant equations are a set of three coupled ordinary differential equations exhibiting chaotic behaviour for certain values of the parameters. They are named after Mikhail Rabinovich and Anatoly Fabrikant, who described them in 1979.
 W
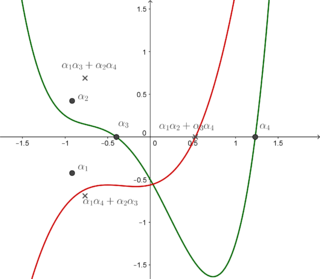
WIn algebra, a resolvent cubic is one of several distinct, although related, cubic polynomials defined from a monic polynomial of degree four:
 W
WThe salvo combat model provides a mathematical representation of anti-ship missile battles between modern warships. It was developed by Wayne Hughes at the U.S. Naval Postgraduate School in Monterey. The salvo model describes the basic elements of modern missile combat in a very simple manner. This is similar to how Lanchester's Square Law provides a simple model of modern gun combat.
 W
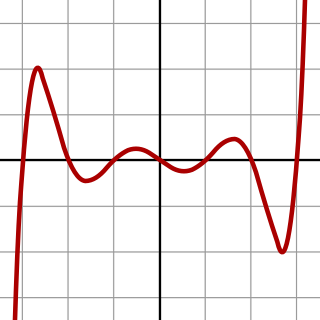
WThe Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium.
 W
WIn algebra, a septic equation is an equation of the form
 W
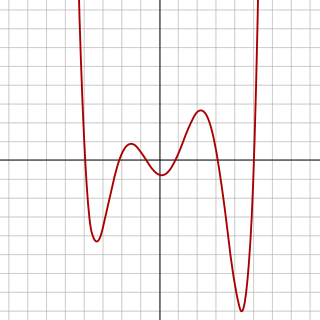
WIn algebra, a sextic polynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:
 W
WThe Souders–Brown equation has been a tool for obtaining the maximum allowable vapor velocity in vapor–liquid separation vessels. It has also been used for the same purpose in designing trayed fractionating columns, trayed absorption columns and other vapor–liquid-contacting columns.
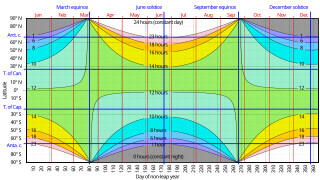 W
WThe sunrise equation can be used to derive the time of sunrise and sunset for any solar declination and latitude in terms of local solar time when sunrise and sunset actually occur. It is:
 W
WIn mathematics, a system of linear equations is a collection of one or more linear equations involving the same set of variables. For example,
 W
WA transcendental equation is an equation containing a transcendental function of the variable(s) being solved for. Such equations often do not have closed-form solutions. Examples include:
 W
WThe Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.
 W
WThe van Deemter equation in chromatography, named for Jan van Deemter, relates the variance per unit length of a separation column to the linear mobile phase velocity by considering physical, kinetic, and thermodynamic properties of a separation. These properties include pathways within the column, diffusion, and mass transfer kinetics between stationary and mobile phases. In liquid chromatography, the mobile phase velocity is taken as the exit velocity, that is, the ratio of the flow rate in ml/second to the cross-sectional area of the ‘column-exit flow path.’ For a packed column, the cross-sectional area of the column exit flow path is usually taken as 0.6 times the cross-sectional area of the column. Alternatively, the linear velocity can be taken as the ratio of the column length to the dead time. If the mobile phase is a gas, then the pressure correction must be applied. The variance per unit length of the column is taken as the ratio of the column length to the column efficiency in theoretical plates. The van Deemter equation is a hyperbolic function that predicts that there is an optimum velocity at which there will be the minimum variance per unit column length and, thence, a maximum efficiency. The van Deemter equation was the result of the first application of rate theory to the chromatography elution process.
 W
WIn relativistic physics, a velocity-addition formula is a three-dimensional equation that relates the velocities of objects in different reference frames. Such formulas apply to successive Lorentz transformations, so they also relate different frames. Accompanying velocity addition is a kinematic effect known as Thomas precession, whereby successive non-collinear Lorentz boosts become equivalent to the composition of a rotation of the coordinate system and a boost.
 W
WThe Wheeler–DeWitt equation is a field equation. It is part of a theory that attempts to combine mathematically the ideas of quantum mechanics and general relativity, a step towards a theory of quantum gravity. In this approach, time plays a role different from what it does in non-relativistic quantum mechanics, leading to the so-called 'problem of time'. More specifically, the equation describes the quantum version of the Hamiltonian constraint using metric variables. Its commutation relations with the diffeomorphism constraints generate the Bergman–Komar "group".