W

Abramowitz and Stegun (AS) is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the United States National Bureau of Standards (NBS), now the National Institute of Standards and Technology (NIST). Its full title is Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. A digital successor to the Handbook was released as the "Digital Library of Mathematical Functions" (DLMF) on May 11, 2010, along with a printed version, the NIST Handbook of Mathematical Functions, published by Cambridge University Press.

W

In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative, and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero.

W

In mathematics, the Barnes G-function G(z) is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function.

W

In mathematics, the Bernoulli polynomials, named after Jacob Bernoulli, combine the Bernoulli numbers and binomial coefficients. They are used for series expansion of functions, and with the Euler–MacLaurin formula.

W

In physics, engineering, and applied mathematics, the Bickley–Naylor functions are a sequence of special functions arising in formulas for thermal radiation intensities in hot enclosures. The solutions are often quite complicated unless the problem is essentially one-dimensional. These functions have practical applications in several engineering problems related to transport of thermal or neutron, radiation in systems with special symmetries. W. G. Bickley was a British mathematician born in 1893.

W

In mathematics, the blancmange curve is a self-affine curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi who described it in 1901, or as the Takagi–Landsberg curve, a generalization of the curve named after Takagi and Georg Landsberg. The name blancmange comes from its resemblance to a pudding of the same name. It is a special case of the more general de Rham curve; see also fractal curve.

W

In mathematics, a boxcar function is any function which is zero over the entire real line except for a single interval where it is equal to a constant, A. The boxcar function can be expressed in terms of the uniform distribution as

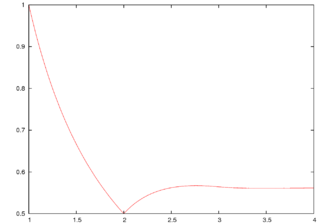
W

The Buchstab function is the unique continuous function  :\mathbb {R} _{\geq 1}\rightarrow \mathbb {R} _{>0}} defined by the delay differential equation

W

In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow, by construction.

W

The Carotid–Kundalini function is closely associated with Carotid-Kundalini fractals coined by popular science columnist Clifford A. Pickover and it is defined as follows:

W

In atmospheric radiation, Chandrasekhar's H-function appears as the solutions of problems involving scattering, introduced by the Indian American astrophysicist Subrahmanyan Chandrasekhar. The Chandrasekhar's H-function defined in the interval , satisfies the following nonlinear integral equation

W

In mathematics, the Coshc function appears frequently in papers about optical scattering, Heisenberg Spacetime and hyperbolic geometry. It is defined as

W

In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson) is the one-sided Fourier–Laplace sine transform of the Gaussian function.

W

In analytic number theory, the Dickman function or Dickman–de Bruijn function ρ is a special function used to estimate the proportion of smooth numbers up to a given bound. It was first studied by actuary Karl Dickman, who defined it in his only mathematical publication, and later studied by the Dutch mathematician Nicolaas Govert de Bruijn.

W

In mathematics, a Dirac comb is a periodic tempered distribution constructed from Dirac delta functions

W

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

W

In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.

W

In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or .

W

The Fresnel integrals S(x) and C(x) are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function. They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations:

W

In mathematics, the Griewank function is often used in testing of optimization, it is defined as follow

W

In mathematics, Hadamard's gamma function, named after Jacques Hadamard, is an extension of the factorial function, different from the classical gamma function. This function, with its argument shifted down by 1, interpolates the factorial and extends it to real and complex numbers in a different way than Euler's gamma function. It is defined as:

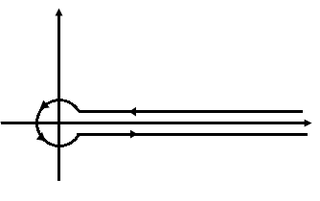
W

In mathematics, a Hankel contour is a path in the complex plane which extends from (+∞,δ), around the origin counter clockwise and back to (+∞,−δ), where δ is an arbitrarily small positive number. The contour thus remains arbitrarily close to the real axis but without crossing the real axis except for negative values of x. The Hankel contour can also be represented by a path that has mirror images just above and below the real axis, connected to a circle of radius ε, centered at the origin, where ε is an arbitrarily small number. The two linear portions of the contour are said to be a distance of δ from the real axis. Thus, the total distance between the linear portions of the contour is 2δ. The contour is traversed in the positively-oriented sense, meaning that the circle around the origin is traversed counter-clockwise.

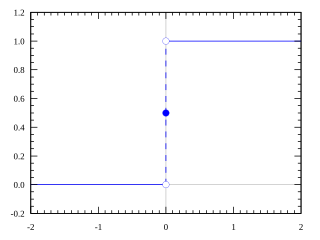
W

The Heaviside step function, or the unit step function, usually denoted by H or θ, is a step function, named after Oliver Heaviside (1850–1925), whose value is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one.

W

The hyperbolastic functions, also known as hyperbolastic growth models, are mathematical functions that are used in medical statistical modeling. These models were originally developed to capture the growth dynamics of multicellular tumor spheres, and were introduced in 2005 by Mohammad Tabatabai, David Williams, and Zoran Bursac. The precision of hyperbolastic functions in modeling real world problems is somewhat due to their flexibility in their point of inflection. These functions can be used in a wide variety of modeling problems such as tumor growth, stem cell proliferation, pharma kinetics, cancer growth, sigmoid activation function in neural networks, and epidemiological disease progression or regression.

W

When a quantity grows towards a singularity under a finite variation it is said to undergo hyperbolic growth. More precisely, the reciprocal function has a hyperbola as a graph, and has a singularity at 0, meaning that the limit as is infinite: any similar graph is said to exhibit hyperbolic growth.

W

In mathematics, the Lambert W function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the inverse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function.

W

A logistic function or logistic curve is a common S-shaped curve with equation

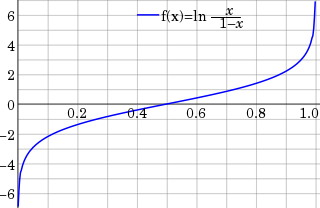
W

In statistics, the logit function or the log-odds is the logarithm of the odds where p is a probability. It is a type of function that creates a map of probability values from to . It is the inverse of the sigmoidal "logistic" function or logistic transform used in mathematics, especially in statistics.

W

The Lommel differential equation is an inhomogeneous form of the Bessel differential equation:

W

In mathematics, the Minkowski question-mark function denoted by ?(x), is a function possessing various unusual fractal properties, defined by Hermann Minkowski. It maps quadratic irrationals to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. In addition, it maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree.

W

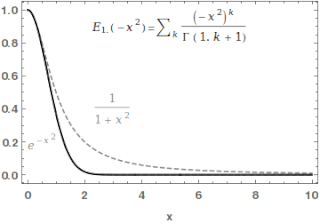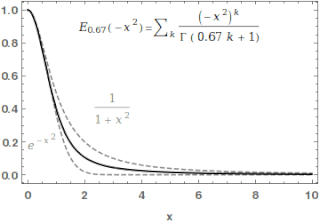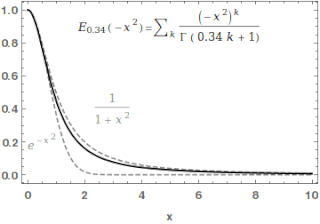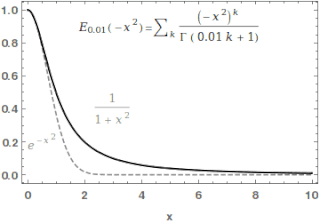
In mathematics, the Mittag-Leffler function Eα,β is a special function, a complex function which depends on two complex parameters α and β. It may be defined by the following series when the real part of α is strictly positive:

W

In mathematics, the Pearcey integral is defined as

W

In mathematics, the Pochhammer contour, introduced by Camille Jordan (1887) and Leo Pochhammer (1890), is a contour in the complex plane with two points removed, used for contour integration. If A and B are loops around the two points, both starting at some fixed point P, then the Pochhammer contour is the commutator ABA−1B−1, where the superscript −1 denotes a path taken in the opposite direction. With the two points taken as 0 and 1, the fixed basepoint P being on the real axis between them, an example is the path that starts at P, encircles the point 1 in the counter-clockwise direction and returns to P, then encircles 0 counter-clockwise and returns to P, after that circling 1 and then 0 clockwise, before coming back to P. The class of the contour is an actual commutator when it is considered in the fundamental group with basepoint P of the complement in the complex plane of the two points looped. When it comes to taking contour integrals, moving basepoint from P to another choice Q makes no difference to the result, since there will be cancellation of integrals from P to Q and back.

W

In mathematics, the polylogarithm is a special function Lis(z) of order s and argument z. Only for special values of s does the polylogarithm reduce to an elementary function such as the natural logarithm or rational functions. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.

W

In statistics, the Q-function is the tail distribution function of the standard normal distribution. In other words, is the probability that a normal (Gaussian) random variable will obtain a value larger than standard deviations. Equivalently, is the probability that a standard normal random variable takes a value larger than .

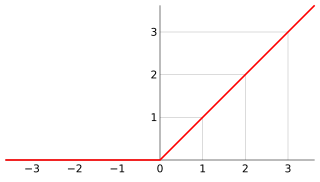
W

The ramp function is a unary real function, whose graph is shaped like a ramp. It can be expressed by numerous definitions, for example "0 for negative inputs, output equals input for non-negative inputs". The term "ramp" can also be used for other functions obtained by scaling and shifting, and the function in this article is the unit ramp function.

W

The rectangular function is defined as

W

In mathematics, the Scorer's functions are special functions studied by Scorer (1950) and denoted Gi(x) and Hi(x).

W

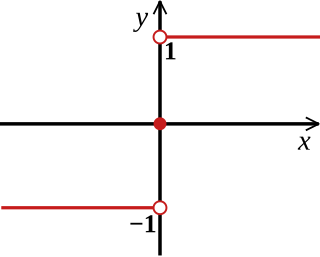
In mathematics, the sign function or signum function is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as sgn.

W

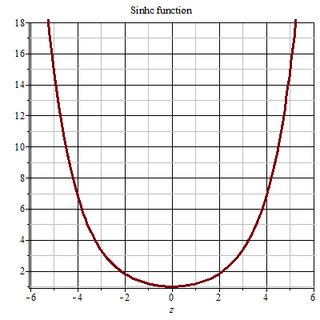
In mathematics, the Sinhc function appears frequently in papers about optical scattering, Heisenberg Spacetime and hyperbolic geometry. It is defined as

W

In mathematics, Spence's function, or dilogarithm, denoted as Li2(z), is a particular case of the polylogarithm. Two related special functions are referred to as Spence's function, the dilogarithm itself:

W

In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces.

W

In mathematics, the Struve functions Hα(x), are solutions y(x) of the non-homogeneous Bessel's differential equation:

W

In probability and statistics, Student's t-distribution is any member of a family of continuous probability distributions that arise when estimating the mean of a normally-distributed population in situations where the sample size is small and the population's standard deviation is unknown. It was developed by English statistician William Sealy Gosset under the pseudonym "Student".

W

In mathematics the synchrotron functions are defined as follows :First synchrotron functionSecond synchrotron function

W

In mathematics, the Tanc function is defined as

W

In mathematics, the tanhc function is defined as

W

Thomae's function, named after Carl Johannes Thomae, has many names: the popcorn function, the raindrop function, the countable cloud function, the modified Dirichlet function, the ruler function, the Riemann function, or the Stars over Babylon. This real-valued function of a real variable can be defined as:

W

The Tracy–Widom distribution, introduced by Craig Tracy and Harold Widom, is the probability distribution of the normalized largest eigenvalue of a random Hermitian matrix.

W

A triangular function is a function whose graph takes the shape of a triangle. Often this is an isosceles triangle of height 1 and base 2 in which case it is referred to as the triangular function. Triangular functions are useful in signal processing and communication systems engineering as representations of idealized signals, and the triangular function specifically as an integral transform kernel function from which more realistic signals can be derived, for example in kernel density estimation. It also has applications in pulse code modulation as a pulse shape for transmitting digital signals and as a matched filter for receiving the signals. It is also used to define the triangular window sometimes called the Bartlett window.

W

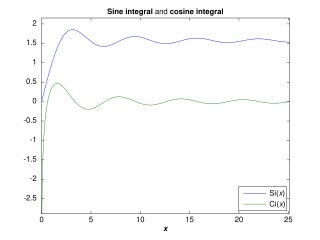
In mathematics, the trigonometric integrals are a family of integrals involving trigonometric functions.

W

The Voigt profile is a probability distribution given by a convolution of a Cauchy-Lorentz distribution and a Gaussian distribution. It is often used in analyzing data from spectroscopy or diffraction.

W

In mathematics, the Wright omega function or Wright function, denoted ω, is defined in terms of the Lambert W function as: