56 History of mathematics

The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, together with Ancient Egypt and Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the patterns in nature, the field of astronomy and to record time and formulate calendars.

Anaxagoras was a Pre-Socratic Greek philosopher. Born in Clazomenae at a time when Asia Minor was under the control of the Persian Empire, Anaxagoras came to Athens. According to Diogenes Laërtius and Plutarch, in later life he was charged with impiety and went into exile in Lampsacus; the charges may have been political, owing to his association with Pericles, if they were not fabricated by later ancient biographers.

The Antikythera mechanism is an ancient Greek hand-powered orrery, described as the first analogue computer, the oldest known example of such a device used to predict astronomical positions and eclipses for calendar and astrological purposes decades in advance. It could also be used to track the four-year cycle of athletic games which was similar to an Olympiad, the cycle of the ancient Olympic Games.

Approximations for the mathematical constant pi in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era (Archimedes). In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century.

Raymond Clare Archibald was a prominent Canadian-American mathematician. He is known for his work as a historian of mathematics, his editorships of mathematical journals and his contributions to the teaching of mathematics.

Aristarchus of Samos was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the known universe with the Earth revolving around it. He was influenced by Philolaus of Croton, but Aristarchus identified the "central fire" with the Sun, and he put the other planets in their correct order of distance around the Sun. Like Anaxagoras before him, he suspected that the stars were just other bodies like the Sun, albeit farther away from Earth. His astronomical ideas were often rejected in favor of the geocentric theories of Aristotle and Ptolemy. Nicolaus Copernicus attributed the heliocentric theory to Aristarchus.

The Arithmeum is a mathematics museum owned by the Forschungsinstitut für Diskrete Mathematik at the University of Bonn.

The Ars Magna is an important Latin-language book on algebra written by Gerolamo Cardano. It was first published in 1545 under the title Artis Magnae, Sive de Regulis Algebraicis Liber Unus. There was a second edition in Cardano's lifetime, published in 1570. It is considered one of the three greatest scientific treatises of the early Renaissance, together with Copernicus' De revolutionibus orbium coelestium and Vesalius' De humani corporis fabrica. The first editions of these three books were published within a two-year span (1543–1545).

Luitzen Egbertus Jan Brouwer, usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, who worked in topology, set theory, measure theory and complex analysis. He is known as the founder of modern topology, particularly for establishing his fixed-point theorem and the topological invariance of dimension.

Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One of these theorems is his "revolutionary discovery" that the set of all real numbers is uncountably, rather than countably, infinite. This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument. The title of the article, "On a Property of the Collection of All Real Algebraic Numbers", refers to its first theorem: the set of real algebraic numbers is countable. Cantor's article was published in 1874. In 1879, he modified his uncountability proof by using the topological notion of a set being dense in an interval.

The table below is a brief chronology of computed numerical values of, or bounds on, the mathematical constant pi. For more detailed explanations for some of these calculations, see Approximations of π.

In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group is either cyclic, or alternating, or it belongs to a broad infinite class called the groups of Lie type, or else it is one of twenty-six or twenty-seven exceptions, called sporadic. Group theory is central to many areas of pure and applied mathematics and the classification theorem has been called one of the great intellectual achievements of humanity. The proof consists of tens of thousands of pages in several hundred journal articles written by about 100 authors, published mostly between 1955 and 2004.

John Corcoran is an American logician, philosopher, mathematician, and historian of logic. He is best known for his philosophical work on concepts such as the nature of inference, relations between conditions, argument-deduction-proof distinctions, the relationship between logic and epistemology, and the place of proof theory and model theory in logic. Nine of Corcoran's papers have been translated into Spanish, Portuguese, Persian, and Arabic; his 1989 "signature" essay was translated into three languages. Fourteen of his papers have been reprinted; one was reprinted twice.

Divina proportione, later also called De divina proportione is a book on mathematics written by Luca Pacioli and illustrated by Leonardo da Vinci, composed around 1498 in Milan and first printed in 1509. Its subject was mathematical proportions and their applications to geometry, to visual art through perspective, and to architecture. The clarity of the written material and Leonardo's excellent diagrams helped the book to achieve an impact beyond mathematical circles, popularizing contemporary geometric concepts and images.

De Prospectiva pingendi is the earliest and only pre-1500 Renaissance treatise solely devoted to the subject of perspective. It was written by the Italian master Piero della Francesca in the mid-1470s to 1480s, and possibly by about 1474. Despite its Latin title, the opus is written in Italian.

Dicaearchus of Messana, also written Dicearchus or Dicearch, was a Greek philosopher, cartographer, geographer, mathematician and author. Dicaearchus was Aristotle's student in the Lyceum. Very little of his work remains extant. He wrote on the history and geography of Greece, of which his most important work was his Life of Greece. He made important contributions to the field of cartography, where he was among the first to use geographical coordinates. He also wrote books on philosophy and politics.

The First Moderns: Profiles in the Origins of Twentieth-Century Thought is a book on Modernism by historian William Everdell, published in 1997 by the University of Chicago Press. A New York Times Notable Book of 1997, and included by the New York Public Library on its list of "25 Books to Remember from 1997," The First Moderns suggests that "the heart of Modernism is the postulate of ontological discontinuity."

Friedrich Ludwig Gottlob Frege was a German philosopher, logician, and mathematician. He worked as a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philosophy, concentrating on the philosophy of language, logic, and mathematics. Though he was largely ignored during his lifetime, Giuseppe Peano (1858–1932), Bertrand Russell (1872–1970), and, to some extent, Ludwig Wittgenstein (1889–1951) introduced his work to later generations of philosophers.

Fundamenta nova theoriae functionum ellipticarum is a book on Jacobi elliptic functions by Carl Gustav Jacob Jacobi. The book was first published in 1829, and has been reprinted in volume 1 of his collected works and on several later occasions. The book introduces Jacobi elliptic functions and the Jacobi triple product identity.

God Created the Integers: The Mathematical Breakthroughs That Changed History is a 2005 anthology, edited by Stephen Hawking, of "excerpts from thirty-one of the most important works in the history of mathematics."

The history of arithmetic includes the period from the emergence of counting before the formal definition of numbers and arithmetic operations over them by means of a system of axioms. Arithmetic — the science of numbers, their properties and their relations — is one of the main mathematical sciences. It is closely connected with algebra and the theory of numbers.

The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. Henry Briggs introduced common logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics.

History of the Theory of Numbers is a three-volume work by L. E. Dickson summarizing work in number theory up to about 1920. The style is unusual in that Dickson mostly just lists results by various authors, with little further discussion. The central topic of quadratic reciprocity and higher reciprocity laws is barely mentioned; this was apparently going to be the topic of a fourth volume that was never written.

Edmund Gustav Albrecht Husserl was a German philosopher who established the school of phenomenology. In his early work, he elaborated critiques of historicism and of psychologism in logic based on analyses of intentionality. In his mature work, he sought to develop a systematic foundational science based on the so-called phenomenological reduction. Arguing that transcendental consciousness sets the limits of all possible knowledge, Husserl redefined phenomenology as a transcendental-idealist philosophy. Husserl's thought profoundly influenced 20th-century philosophy, and he remains a notable figure in contemporary philosophy and beyond.

In mathematics, infinitesimals or infinitesimal numbers are quantities that are closer to zero than any standard real number, but are not zero. They do not exist in the standard real number system, but do exist in many other number systems, such as the surreal numbers and hyperreal numbers, which can be thought of as the real numbers augmented with a system of infinitesimal quantities, as well as infinite quantities, which are the reciprocals of the infinitesimals.

The Ishango bone is a bone tool and possible mathematical object, dated to the Upper Paleolithic era. It is a dark brown length of bone, the fibula of a baboon, with a sharp piece of quartz affixed to one end, perhaps for engraving. It is thought by some to be a tally stick, as it has a series of what has been interpreted as tally marks carved in three columns running the length of the tool, though it has also been suggested that the scratches might have been to create a better grip on the handle or for some other non-mathematical reason. It has also been argued that the marks on the object are non-random and that it was likely a kind of counting tool and used to perform simple mathematical procedures.

The Kerala school of astronomy and mathematics or the Kerala school was a school of mathematics and astronomy founded by Madhava of Sangamagrama in Kerala, India which included among its members: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri and Achyuta Panikkar. The school flourished between the 14th and 16th centuries and the original discoveries of the school seems to have ended with Narayana Bhattathiri (1559–1632). In attempting to solve astronomical problems, the Kerala school independently discovered a number of important mathematical concepts. Their most important results—series expansion for trigonometric functions—were described in Sanskrit verse in a book by Neelakanta called Tantrasangraha, and again in a commentary on this work, called Tantrasangraha-vakhya, of unknown authorship. The theorems were stated without proof, but proofs for the series for sine, cosine, and inverse tangent were provided a century later in the work Yuktibhasa, written in Malayalam, by Jyesthadeva, and also in a commentary on Tantrasangraha.

Gottfried Wilhelm (von) Leibniz was a prominent German polymath and one of the most important logicians, mathematicians and natural philosophers of the Enlightenment. As a representative of the seventeenth-century tradition of rationalism, Leibniz developed, as his most prominent accomplishment, the ideas of differential and integral calculus, independently of Isaac Newton's contemporaneous developments. Mathematical works have consistently favored Leibniz's notation as the conventional expression of calculus. It was only in the 20th century that Leibniz's law of continuity and transcendental law of homogeneity found mathematical implementation. He became one of the most prolific inventors in the field of mechanical calculators. While working on adding automatic multiplication and division to Pascal's calculator, he was the first to describe a pinwheel calculator in 1685 and invented the Leibniz wheel, used in the arithmometer, the first mass-produced mechanical calculator. He also refined the binary number system, which is the foundation of nearly all digital computers, including the Von Neumann machine, which is the standard design paradigm, or "computer architecture", followed from the second half of the 20th century, and into the 21st.

Logic is the systematic study of valid rules of inference, i.e. the relations that lead to the acceptance of one proposition on the basis of a set of other propositions (premises). More broadly, logic is the analysis and appraisal of arguments.

The Lwów school of mathematics was a group of Polish mathematicians who worked in the interwar period in Lwów, Poland. The mathematicians often met at the famous Scottish Café to discuss mathematical problems, and published in the journal Studia Mathematica, founded in 1929. The school was renowned for its productivity and its extensive contributions to subjects such as point-set topology, set theory and functional analysis. The biographies and contributions of these mathematicians were documented in 1980 by their contemporary Kazimierz Kuratowski in his book A Half Century of Polish Mathematics: Remembrances and Reflections.

Salomon Maimon was a philosopher born of Lithuanian Jewish parentage in the Grand Duchy of Lithuania, present-day Belarus. Some of his work was written in the German language.

Mathematical tables are lists of numbers showing the results of a calculation with varying arguments. Tables of trigonometric functions were used in ancient Greece and India for applications to astronomy and celestial navigation. They continued to be widely used until electronic calculators became cheap and plentiful, in order to simplify and drastically speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks, and specialized tables were published for numerous applications.

Method of Fluxions is a book by Isaac Newton. The book was completed in 1671, and published in 1736. Fluxion is Newton's term for a derivative. He originally developed the method at Woolsthorpe Manor during the closing of Cambridge during the Great Plague of London from 1665 to 1667, but did not choose to make his findings known. Gottfried Leibniz developed his form of calculus independently around 1673, 7 years after Newton had developed the basis for differential calculus, as seen in surviving documents like “the method of fluxions and fluents..." from 1666. Leibniz however published his discovery of differential calculus in 1684, nine years before Newton formally published his fluxion notation form of calculus in part during 1693. The calculus notation in use today is mostly that of Leibniz, although Newton's dot notation for differentiation for denoting derivatives with respect to time is still in current use throughout mechanics and circuit analysis.

Milü, also known as Zulü, is the name given to an approximation to π (pi) found by Chinese mathematician and astronomer, Zǔ Chōngzhī (祖沖之), born 429 AD. Using Liu Hui's algorithm, Zu famously computed π to be between 3.1415926 and 3.1415927 and gave two rational approximations of π, 22/7 and 355/113, naming them respectively Yuelü 约率 and Milü.

MiMa is a museum of mineralogy and mathematics in Oberwolfach, in the central Black Forest in southern Germany. The museum was opened on 30 January 2010 on the site of the mineral museum after a two-year conversion and expansion phase. It is operated jointly by the municipality of Oberwolfach, the Oberwolfach Society of the Friends of Minerals and Mining and the Mathematics Research Institute, Oberwolfach.

A pattern is a regularity in the world, in human-made design, or in abstract ideas. As such, the elements of a pattern repeat in a predictable manner. A geometric pattern is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design.

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime.

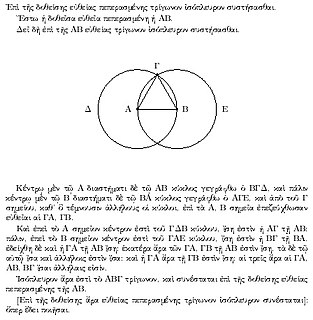
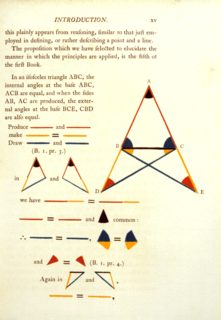
In geometry, the statement that the angles opposite the equal sides of an isosceles triangle are themselves equal is known as the pons asinorum, typically translated as "bridge of asses". This statement is Proposition 5 of Book 1 in Euclid's Elements, and is also known as the isosceles triangle theorem. Its converse is also true: if two angles of a triangle are equal, then the sides opposite them are also equal. The term is also applied to the Pythagorean Theorem.

The Quadrature of the Parabola is a treatise on geometry, written by Archimedes in the 3rd century BC. Written as a letter to his friend Dositheus, the work presents 24 propositions regarding parabolas, culminating in a proof that the area of a parabolic segment is 4/3 that of a certain inscribed triangle.

Willard van Orman Quine was an American philosopher and logician in the analytic tradition, recognized as "one of the most influential philosophers of the twentieth century." From 1930 until his death 70 years later, Quine was continually affiliated with Harvard University in one way or another, first as a student, then as a professor. He filled the Edgar Pierce Chair of Philosophy at Harvard from 1956 to 1978.

Regiomontanus' angle maximization problem

In mathematics, the Regiomontanus's angle maximization problem, is a famous optimization problem posed by the 15th-century German mathematician Johannes Müller. The problem is as follows:

The relationship between mathematics and physics has been a subject of study of philosophers, mathematicians and physicists since Antiquity, and more recently also by historians and educators. Generally considered a relationship of great intimacy, mathematics has been described as "an essential tool for physics" and physics has been described as "a rich source of inspiration and insight in mathematics".

Bertrand Arthur William Russell, 3rd Earl Russell was a British polymath, philosopher, logician, mathematician, historian, writer, social critic, political activist, and Nobel laureate. Throughout his life, Russell considered himself a liberal, a socialist and a pacifist, although he sometimes suggested that his sceptical nature had led him to feel that he had "never been any of these things, in any profound sense". Russell was born in Monmouthshire into one of the most prominent aristocratic families in the United Kingdom.

A sand table uses constrained sand for modelling or educational purposes. The original version of a sand table may be the abax used by early Greek students. In the modern era, one common use for a sand table is to make terrain models for military planning and wargaming.

The Scottish Book was a thick notebook used by mathematicians of the Lwów School of Mathematics in Poland for jotting down problems meant to be solved. The notebook was named after the "Scottish Café" where it was kept.

The Scottish Café was a café in Lwów, Poland where, in the 1930s and 1940s, mathematicians from the Lwów School of Mathematics collaboratively discussed research problems, particularly in functional analysis and topology.

The Story of Maths is a four-part British television series outlining aspects of the history of mathematics. It was a co-production between the Open University and the BBC and aired in October 2008 on BBC Four. The material was written and presented by University of Oxford professor Marcus du Sautoy. The consultants were the Open University academics Robin Wilson, professor Jeremy Gray and June Barrow-Green. Kim Duke is credited as series producer.

Summa de arithmetica, geometria, proportioni et proportionalita is a book on mathematics written by Luca Pacioli and first published in 1494. It contains a comprehensive summary of Renaissance mathematics, including practical arithmetic, basic algebra, basic geometry and accounting, written for use as a textbook and reference work.

Alfred Tarski, born Alfred Teitelbaum, was a Polish-American logician and mathematician. A prolific author best known for his work on model theory, metamathematics, and algebraic logic, he also contributed to abstract algebra, topology, geometry, measure theory, mathematical logic, set theory, and analytic philosophy.

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics and reaching its modern form with Leonhard Euler (1748).

John Wallis was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal court. He is credited with introducing the symbol ∞ to represent the concept of infinity. He similarly used 1/∞ for an infinitesimal. John Wallis was a contemporary of Newton and one of the greatest intellectuals of the early renaissance of mathematics.

The Whetstone of Witte is the shortened title of Robert Recorde's mathematics book published in 1557, the full title being The whetstone of witte, whiche is the seconde parte of Arithmetike: containyng thextraction of Rootes: The Coßike practise, with the rule of Equation: and the woorkes of Surde Nombers. The book covers topics including whole numbers, the extraction of roots and irrational numbers. The work is notable for containing the first recorded use of the equals sign and also for being the first book in English to use the plus and minus signs.

Alfred North Whitehead was an English mathematician and philosopher. He is best known as the defining figure of the philosophical school known as process philosophy, which today has found application to a wide variety of disciplines, including ecology, theology, education, physics, biology, economics, and psychology, among other areas.

The questions pertaining to "why there is anything at all?", or, "why there is something rather than nothing" has been raised or commented on by philosophers including Gottfried Wilhelm Leibniz, Ludwig Wittgenstein, and Martin Heidegger – who called it "the fundamental question of metaphysics".

A tally stick was an ancient memory aid device used to record and document numbers, quantities, or even messages. Tally sticks first appear as animal bones carved with notches during the Upper Palaeolithic; a notable example is the Ishango Bone. Historical reference is made by Pliny the Elder about the best wood to use for tallies, and by Marco Polo (1254–1324) who mentions the use of the tally in China. Tallies have been used for numerous purposes such as messaging and scheduling, and especially in financial and legal transactions, to the point of being currency.

Zenzizenzizenzic is an obsolete form of mathematical notation representing the eighth power of a number, dating from a time when powers were written out in words rather than as superscript numbers. This term was suggested by Robert Recorde, a 16th-century Welsh writer of popular mathematics textbooks, in his 1557 work The Whetstone of Witte ; he wrote that it "doeth represent the square of squares squaredly".