WTrigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios such as sine.
WThe Abbe sine condition is a condition that must be fulfilled by a lens or other optical system in order for it to produce sharp images of off-axis as well as on-axis objects. It was formulated by Ernst Abbe in the context of microscopes.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn mathematics, the argument is a multi-valued function operating on the nonzero complex numbers. With complex numbers z visualized as a point in the complex plane, the argument of z is the angle between the positive real axis and the line joining the point to the origin, shown as in Figure 1 and denoted arg z. To define a single-valued function, the principal value of the argument is used. It is often chosen to be the unique value of the argument that lies within the interval (–π, π].
WThe astronomical treatise Āryabhaṭīya was composed during the fifth century by the Indian mathematician and astronomer Āryabhaṭa, for the computation of the half-chords of certain set of arcs of a circle. It is not a table in the modern sense of a mathematical table; that is, it is not a set of numbers arranged into rows and columns.
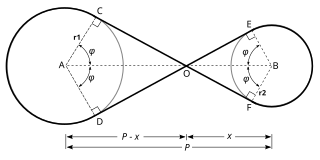
WThe belt problem is a mathematics problem which requires finding the length of a crossed belt that connects two circular pulleys with radius r1 and r2 whose centers are separated by a distance P. The solution of the belt problem requires trigonometry and the concepts of the bitangent line, the vertical angle, and congruent angles.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn mathematics, a function f is cofunction of a function g if f(A) = g(B) whenever A and B are complementary angles. This definition typically applies to trigonometric functions. The prefix "co-" can be found already in Edmund Gunter's Canon triangulorum (1620).
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WEquant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of the planets. The equant is used to explain the observed speed change in different stages of the planetary orbit. This planetary concept allowed Ptolemy to keep the theory of uniform circular motion alive by stating that the path of heavenly bodies was uniform around one point and circular around another point.
WIn estimation theory, estimation of signal parameters via rotational invariant techniques (ESPRIT) is a technique to determine parameters of a mixture of sinusoids in a background noise. This technique is first proposed for frequency estimation, however, with the introduction of phased-array systems in daily use technology, it is also used for Angle of arrival estimations as well.
WEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number x:
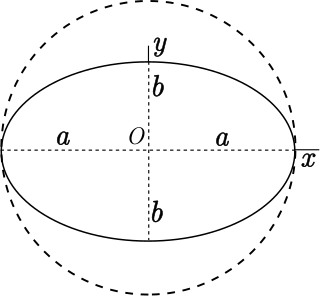
WFlattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is f and its definition in terms of the semi-axes of the resulting ellipse or ellipsoid is
WOrdinary trigonometry studies triangles in the Euclidean plane R2. There are a number of ways of defining the ordinary Euclidean geometric trigonometric functions on real numbers: right-angled triangle definitions, unit-circle definitions, series definitions, definitions via differential equations, definitions using functional equations. Generalizations of trigonometric functions are often developed by starting with one of the above methods and adapting it to a situation other than the real numbers of Euclidean geometry. Generally, trigonometry can be the study of triples of points in any kind of geometry or space. A triangle is the polygon with the smallest number of vertices, so one direction to generalize is to study higher-dimensional analogs of angles and polygons: solid angles and polytopes such as tetrahedrons and n-simplices.
WIn mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena, through Fourier analysis.
WIn crystallography, a Greninger chart is a chart that allows angular relations between zones and planes in a crystal to be directly read from an x-ray diffraction photograph.
WThe Gudermannian function, named after Christoph Gudermann (1798–1852), relates the circular functions and hyperbolic functions without explicitly using complex numbers.
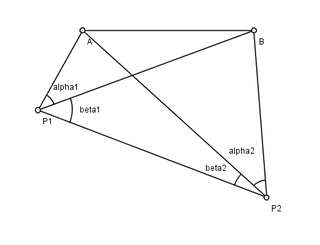
WHansen's problem is a problem in planar surveying, named after the astronomer Peter Andreas Hansen (1795–1874), who worked on the geodetic survey of Denmark. There are two known points A and B, and two unknown points P1 and P2. From P1 and P2 an observer measures the angles made by the lines of sight to each of the other three points. The problem is to find the positions of P1 and P2. See figure; the angles measured are (α1, β1, α2, β2).
WEarly study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics and reaching its modern form with Leonhard Euler (1748).
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. For example, if one of the other sides has a length of 3 and the other has a length of 4, then their squares add up to 25. The length of the hypotenuse is the square root of 25, that is, 5.
WIn mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
WBürgi's Kunstweg is a set of algorithms invented by Jost Bürgi at the end of the 16th century. They can be used for the calculation of sines to an arbitrary precision. Bürgi used these algorithms to calculate a Canon Sinuum, a table of sines in steps of 2 arc seconds. It is thought that this table had 8 sexagesimal places. Some authors have speculated that this table only covered the range from 0 to 45 degrees, but nothing seems to support this claim. Such tables were extremely important for navigation at sea. Johannes Kepler called the Canon Sinuum the most precise known table of sines. Bürgi explained his algorithms in his work Fundamentum Astronomiae which he presented to Emperor Rudolf II. in 1592.
WIn trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states
WIn trigonometry, the law of cotangents is a relationship among the lengths of the sides of a triangle and the cotangents of the halves of the three angles.
WIn trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. According to the law,
WIn trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.
WA Lénárt sphere is a teaching and educational research model for spherical geometry. The Lénárt sphere is a modern replacement of a "spherical blackboard". It can be used for visualizing spherical polygons showing the relationships between the sides and the angles.
WA Lissajous curve, also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equations
WIn orbital mechanics, a Lissajous orbit, named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbits around a Lagrangian point are curved paths that lie entirely in the plane of the two primary bodies. In contrast, Lissajous orbits include components in this plane and perpendicular to it, and follow a Lissajous curve. Halo orbits also include components perpendicular to the plane, but they are periodic, while Lissajous orbits are not.
WThe following is a list of integrals of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antiderivative functions, see Lists of integrals. For the special antiderivatives involving trigonometric functions, see Trigonometric integral.
WIn mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn trigonometry, Mollweide's formula, sometimes referred to in older texts as Mollweide's equations, named after Karl Mollweide, is a set of two relationships between sides and angles in a triangle.
WParallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. Due to foreshortening, nearby objects show a larger parallax than farther objects when observed from different positions, so parallax can be used to determine distances.
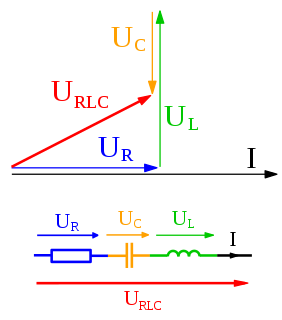
WIn physics and engineering, a phasor, is a complex number representing a sinusoidal function whose amplitude (A), angular frequency (ω), and initial phase (θ) are time-invariant. It is related to a more general concept called analytic representation, which decomposes a sinusoid into the product of a complex constant and a factor that encapsulates the frequency and time dependence. The complex constant, which encapsulates amplitude and phase dependence, is known as phasor, complex amplitude, and sinor or even complexor.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn mathematics, the Regiomontanus's angle maximization problem, is a famous optimization problem posed by the 15th-century German mathematician Johannes Müller. The problem is as follows:
WThe rule of marteloio is a medieval technique of navigational computation that uses compass direction, distance and a simple trigonometric table known as the toleta de marteloio. The rule told mariners how to plot the traverse between two different navigation courses by means of resolving triangles with the help of the Toleta and basic arithmetic.
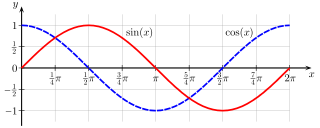
WA sine wave or sinusoid is a mathematical curve that describes a smooth periodic oscillation. A sine wave is a continuous wave. It is named after the function sine, of which it is the graph. It occurs often in both pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. Its most basic form as a function of time (t) is:
WThe small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
WThe Snellius–Pothenot problem is a problem in planar surveying. Given three known points A, B and C, an observer at an unknown point P observes that the segment AC subtends an angle and the segment CB subtends an angle ; the problem is to determine the position of the point P..
WThe space cardioid is a 3-dimensional curve derived from the cardioid. It has a parametric representation using trigonometric functions.
WExact algebraic expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification.
WIn mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena, through Fourier analysis.
WIn mathematics, the trigonometric integrals are a family of integrals involving trigonometric functions.
WIn mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. In calculus, trigonometric substitution is a technique for evaluating integrals. Moreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.
WIn mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables was an important area of study, which led to the development of the first mechanical computing devices.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.
WIn mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as S1 because it is a one-dimensional unit n-sphere.
WAmongst the lay public of non-mathematicians and non-scientists, trigonometry is known chiefly for its application to measurement problems, yet is also often used in ways that are far more subtle, such as its place in the theory of music; still other uses are more technical, such as in number theory. The mathematical topics of Fourier series and Fourier transforms rely heavily on knowledge of trigonometric functions and find application in a number of areas, including statistics.
WCORDIC, also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC, Linear CORDIC, Hyperbolic CORDIC, and Generalized Hyperbolic CORDIC, is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available, as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is often used to implement floating-point arithmetic when the target platform lacks hardware multiply for cost or space reasons.