W

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing to group theory certain problems in field theory; this makes them simpler in some sense, and allows a better understanding.

W

In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is well-defined up to inner automorphism. It is a profinite group.

W

In number theory, the Elkies trinomial curves are certain hyperelliptic curves constructed by Noam Elkies which have the property that rational points on them correspond to trinomial polynomials giving an extension of Q with particular Galois groups.

W

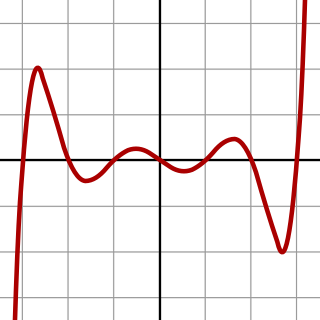
In algebra, a quintic function is a function of the form

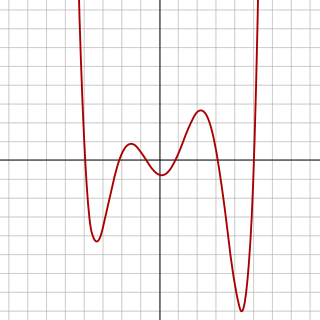
W

In algebra, a septic equation is an equation of the form

W

In algebra, a sextic polynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:

W

Wiles's proof of Fermat's Last Theorem is a proof by British mathematician Andrew Wiles of a special case of the modularity theorem for elliptic curves. Together with Ribet's theorem, it provides a proof for Fermat's Last Theorem. Both Fermat's Last Theorem and the modularity theorem were almost universally considered inaccessible to proof by contemporaneous mathematicians, meaning that they were believed to be impossible to prove using current knowledge.