 W
WIn statistics, Fisher's method, also known as Fisher's combined probability test, is a technique for data fusion or "meta-analysis". It was developed by and named for Ronald Fisher. In its basic form, it is used to combine the results from several independent tests bearing upon the same overall hypothesis (H0).
 W
WIn statistics, the Goldfeld–Quandt test checks for homoscedasticity in regression analyses. It does this by dividing a dataset into two parts or groups, and hence the test is sometimes called a two-group test. The Goldfeld–Quandt test is one of two tests proposed in a 1965 paper by Stephen Goldfeld and Richard Quandt. Both a parametric and nonparametric test are described in the paper, but the term "Goldfeld–Quandt test" is usually associated only with the former.
 W
WIn statistics, the Kolmogorov–Smirnov test is a nonparametric test of the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution, or to compare two samples. It is named after Andrey Kolmogorov and Nikolai Smirnov.
 W
WIn statistical significance testing, a one-tailed test and a two-tailed test are alternative ways of computing the statistical significance of a parameter inferred from a data set, in terms of a test statistic. A two-tailed test is appropriate if the estimated value is greater or less than a certain range of values, for example, whether a test taker may score above or below a specific range of scores. This method is used for null hypothesis testing and if the estimated value exists in the critical areas, the alternative hypothesis is accepted over the null hypothesis. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, left or right, but not both. An example can be whether a machine produces more than one-percent defective products. In this situation, if the estimated value exists in one of the one-sided critical areas, depending on the direction of interest, the alternative hypothesis is accepted over the null hypothesis. Alternative names are one-sided and two-sided tests; the terminology "tail" is used because the extreme portions of distributions, where observations lead to rejection of the null hypothesis, are small and often "tail off" toward zero as in the normal distribution, colored in yellow, or "bell curve", pictured on the right and colored in green.
 W
WIn statistics, Spearman's rank correlation coefficient or Spearman's ρ, named after Charles Spearman and often denoted by the Greek letter (rho) or as , is a nonparametric measure of rank correlation. It assesses how well the relationship between two variables can be described using a monotonic function.
 W
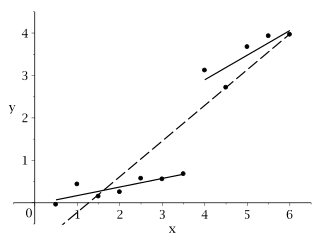
WIn econometrics and statistics, a structural break is an unexpected change over time in the parameters of regression models, which can lead to huge forecasting errors and unreliability of the model in general. This issue was popularised by David Hendry, who argued that lack of stability of coefficients frequently caused forecast failure, and therefore we must routinely test for structural stability. Structural stability − i.e., the time-invariance of regression coefficients − is a central issue in all applications of linear regression models.
 W
WA Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Z-test tests the mean of a distribution. For each significance level in the confidence interval, the Z-test has a single critical value which makes it more convenient than the Student's t-test whose critical values are defined by the sample size.