 W
WIn differential geometry, Fenchel's theorem states that the average curvature of any closed convex plane curve is
 W
WThe classical four-vertex theorem of geometry states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.
 W
WIn mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.
 W
WThe Gauss–Bonnet theorem, or Gauss–Bonnet formula, is a relationship between surfaces in differential geometry. It connects the curvature of a surface to its Euler characteristic.
 W
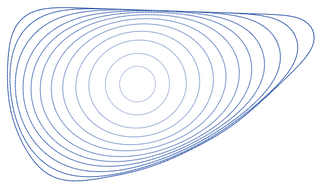
WIn differential geometry, the Tait–Kneser theorem states that, if a smooth plane curve has monotonic curvature, then the osculating circles of the curve are disjoint and nested within each other. The logarithmic spiral or the pictured Archimedean spiral provide examples of curves whose curvature is monotonic for the entire curve. This monotonicity cannot happen for a simple closed curve but for such curves the theorem can be applied to the arcs of the curves between its vertices.
 W
WIn geometry, the tennis ball theorem states that any smooth curve on the surface of a sphere that divides the sphere into two equal-area subsets without touching or crossing itself must have at least four inflection points, points at which the curve does not consistently bend to only one side of its tangent line. The tennis ball theorem was first published under this name by Vladimir Arnold in 1994, and is often attributed to Arnold, but a closely related result appears earlier in a 1968 paper by Beniamino Segre, and the tennis ball theorem itself is a special case of a theorem in a 1977 paper by Joel L. Weiner. The name of the theorem comes from the standard shape of a tennis ball, whose seam forms a curve that meets the conditions of the theorem; the same kind of curve is also used for the seams on baseballs.
 W
WIn differential geometry, the Willmore conjecture is a lower bound on the Willmore energy of a torus. It is named after the English mathematician Tom Willmore, who conjectured it in 1965. A proof by Fernando Codá Marques and André Neves was announced in 2012 and published in 2014.