 W
WIn mathematics, a discrete subgroup of a topological group G is a subgroup H such that there is an open cover of G in which every open subset contains exactly one element of H ; in other words, the subspace topology of H in G is the discrete topology. For example, the integers, Z, form a discrete subgroup of the reals, R, but the rational numbers, Q, do not. A discrete group is a topological group G equipped with the discrete topology.
 W
WIn mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root systems were used by Kac and Moody in their work on Kac–Moody algebras. Possibly non-reduced affine root systems were introduced and classified by Macdonald (1972) and Bruhat & Tits (1972).
 W
WIn mathematics, a frieze or frieze pattern is a design on a two-dimensional surface that is repetitive in one direction. Such patterns occur frequently in architecture and decorative art. A frieze group is the set of symmetries of a frieze pattern, specifically the set of isometries of the pattern, that is geometric transformations built from rigid motions and reflections that preserve the pattern. The mathematical study of frieze patterns reveals that they can be classified into seven types according to their symmetries.
 W
WIn mathematics, a Kleinian group is a discrete subgroup of PSL(2, C). The group PSL(2, C) of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic space H3, and as orientation-preserving conformal maps of the open unit ball B3 in R3 to itself. Therefore, a Kleinian group can be regarded as a discrete subgroup acting on one of these spaces.
 W
WIn geometry and group theory, a lattice in is a subgroup of the additive group which is isomorphic to the additive group , and which spans the real vector space . In other words, for any basis of , the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice. A lattice may be viewed as a regular tiling of a space by a primitive cell.
 W
WIn mathematics, a Schottky group is a special sort of Kleinian group, first studied by Friedrich Schottky (1877).
 W
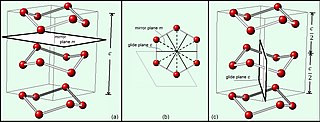
WIn mathematics, physics and chemistry, a space group is the symmetry group of a configuration in space, usually in three dimensions. In three dimensions, there are 219 distinct types, or 230 if chiral copies are considered distinct. Space groups are also studied in dimensions other than 3 where they are sometimes called Bieberbach groups, and are discrete cocompact groups of isometries of an oriented Euclidean space.
 W
WA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles and tiles as well as wallpaper.