W

In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.

W

In geometry, an Archimedean circle is any circle constructed from an arbelos that has the same radius as each of Archimedes' twin circles. If the arbelos is normed such that the diameter of its outer (largest) half circle has a length of 1 and r denotes the radiius of any of the inner half circles, then the radius ρ of such an Archimedean circle is given by

W

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.

W

In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff in 1974.

W

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions (lemmas) on circles.

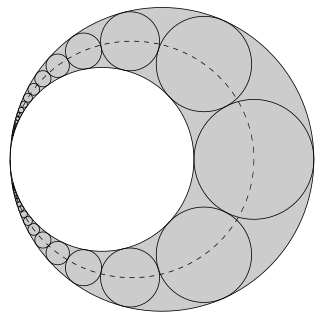
W

In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.

W

In geometry, the Schoch line is a line defined from an arbelos and named by Peter Woo after Thomas Schoch, who had studied it in conjunction with the Schoch circles.

W

In geometry, the twin circles are two special circles associated with an arbelos. An arbelos is determined by three collinear points A, B, and C, and is the curvilinear triangular region between the three semicircles that have AB, BC, and AC as their diameters. If the arbelos is partitioned into two smaller regions by a line segment through the middle point of A, B, and C, perpendicular to line ABC, then each of the two twin circles lies within one of these two regions, tangent to its two semicircular sides and to the splitting segment.

W

In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.