W

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

W

In graph theory, the bipartite half or half-square of a bipartite graph G = (U,V,E) is a graph whose vertex set is one of the two sides of the bipartition and in which there is an edge uiuj for each two vertices ui and uj in U that are at distance two from each other in G. That is, in a more compact notation, the bipartite half is G2[U] where the superscript 2 denotes the square of a graph and the square brackets denote an induced subgraph.

W

In graph-theoretic mathematics, a biregular graph or semiregular bipartite graph is a bipartite graph for which every two vertices on the same side of the given bipartition have the same degree as each other. If the degree of the vertices in is and the degree of the vertices in is , then the graph is said to be -biregular.

W

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

W

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.

W

In graph theory, a branch of mathematics, the modular graphs are undirected graphs in which every three vertices x, y, and z have at least one median vertex m(x,y,z) that belongs to shortest paths between each pair of x, y, and z. Their name comes from the fact that a finite lattice is a modular lattice if and only if its Hasse diagram is a modular graph.

W

In graph theory, a branch of mathematics, the simplex graph κ(G) of an undirected graph G is itself a graph, with one node for each clique in G. Two nodes of κ(G) are linked by an edge whenever the corresponding two cliques differ in the presence or absence of a single vertex.

W

In graph theory, a branch of mathematics, a squaregraph is a type of undirected graph that can be drawn in the plane in such a way that every bounded face is a quadrilateral and every vertex with three or fewer neighbors is incident to an unbounded face.

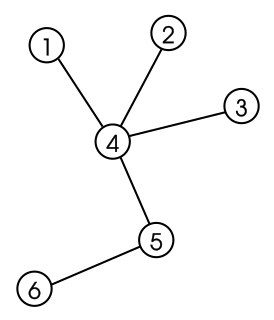
W

In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.