 W
WIn mathematics, an integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.
 W
WIn calculus, Cavalieri's quadrature formula, named for 17th-century Italian mathematician Bonaventura Cavalieri, is the integral
 W
WIn mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
 W
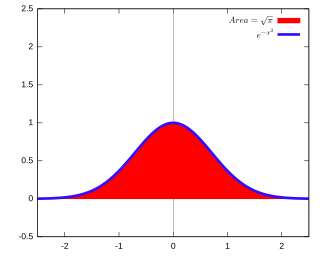
WThe Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
 W
WIn mathematics, the logarithmic integral function or integral logarithm li(x) is a special function. It is relevant in problems of physics and has number theoretic significance. In particular, according to the Siegel-Walfisz theorem it is a very good approximation to the prime-counting function, which is defined as the number of prime numbers less than or equal to a given value .
 W
WThe path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
 W
WIn mathematics, an integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.
 W
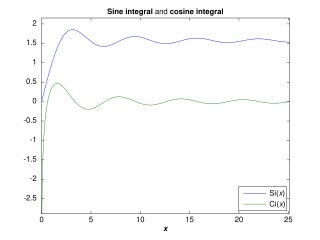
WIn mathematics, the trigonometric integrals are a family of integrals involving trigonometric functions.
 W
WVisual calculus, invented by Mamikon Mnatsakanian, is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner calls "aha! solutions" or Roger Nelsen a proof without words.