 W
WA mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. An unproven proposition that is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.
 W
WIn set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument, the anti-diagonal argument, or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers. Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
 W
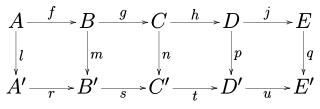
WIn mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.
 W
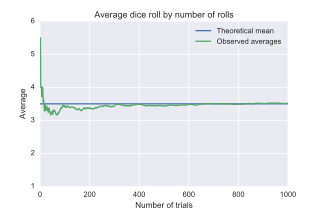
WIn probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed.
 W
WThe proof of Gödel's completeness theorem given by Kurt Gödel in his doctoral dissertation of 1929 is not easy to read today; it uses concepts and formalisms that are no longer used and terminology that is often obscure. The version given below attempts to represent all the steps in the proof and all the important ideas faithfully, while restating the proof in the modern language of mathematical logic. This outline should not be considered a rigorous proof of the theorem.
 W
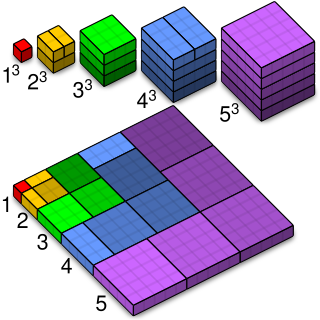
WIn mathematics, a proof without words is a proof of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than formal or mathematically rigorous due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable.
 W
WIn mathematics, a theorem is a non-self-evident statement that has been proven to be true, either on the basis of generally accepted statements such as axioms or on the basis of previously established statements such as other theorems. A theorem is hence a logical consequence of the axioms, with a proof of the theorem being a logical argument which establishes its truth through the inference rules of a deductive system. As a result, the proof of a theorem is often interpreted as justification of the truth of the theorem statement. In light of the requirement that theorems be proved, the concept of a theorem is fundamentally deductive, in contrast to the notion of a scientific law, which is experimental.
 W
WIn mathematics, the tombstone, halmos, end-of-proof, or Q.E.D. symbol "∎" is a symbol used to denote the end of a proof, in place of the traditional abbreviation "Q.E.D." for the Latin phrase "quod erat demonstrandum", meaning "which was to be demonstrated". In magazines, it is one of the various symbols used to indicate the end of an article.
 W
WWiles's proof of Fermat's Last Theorem is a proof by British mathematician Andrew Wiles of a special case of the modularity theorem for elliptic curves. Together with Ribet's theorem, it provides a proof for Fermat's Last Theorem. Both Fermat's Last Theorem and the modularity theorem were almost universally considered inaccessible to proof by contemporaneous mathematicians, meaning that they were believed to be impossible to prove using current knowledge.