9 Monte Carlo methods

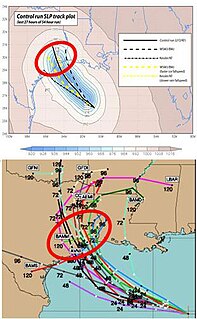
Ensemble forecasting is a method used in or within numerical weather prediction. Instead of making a single forecast of the most likely weather, a set of forecasts is produced. This set of forecasts aims to give an indication of the range of possible future states of the atmosphere. Ensemble forecasting is a form of Monte Carlo analysis. The multiple simulations are conducted to account for the two usual sources of uncertainty in forecast models: (1) the errors introduced by the use of imperfect initial conditions, amplified by the chaotic nature of the evolution equations of the atmosphere, which is often referred to as sensitive dependence on initial conditions; and (2) errors introduced because of imperfections in the model formulation, such as the approximate mathematical methods to solve the equations. Ideally, the verified future atmospheric state should fall within the predicted ensemble spread, and the amount of spread should be related to the uncertainty (error) of the forecast. In general, this approach can be used to make probabilistic forecasts of any dynamical system, and not just for weather prediction.

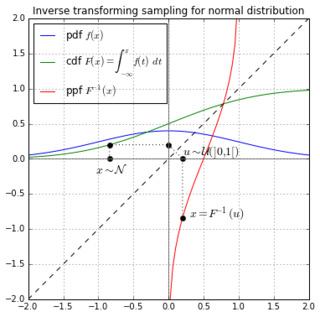
Inverse transform sampling is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function.

In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. This sequence can be used to approximate the distribution or to compute an integral. Metropolis–Hastings and other MCMC algorithms are generally used for sampling from multi-dimensional distributions, especially when the number of dimensions is high. For single-dimensional distributions, there are usually other methods that can directly return independent samples from the distribution, and these are free from the problem of autocorrelated samples that is inherent in MCMC methods.

In mathematics, Monte Carlo integration is a technique for numerical integration using random numbers. It is a particular Monte Carlo method that numerically computes a definite integral. While other algorithms usually evaluate the integrand at a regular grid, Monte Carlo randomly chooses points at which the integrand is evaluated. This method is particularly useful for higher-dimensional integrals.

Modeling photon propagation with Monte Carlo methods is a flexible yet rigorous approach to simulate photon transport. In the method, local rules of photon transport are expressed as probability distributions which describe the step size of photon movement between sites of photon-tissue interaction and the angles of deflection in a photon's trajectory when a scattering event occurs. This is equivalent to modeling photon transport analytically by the radiative transfer equation (RTE), which describes the motion of photons using a differential equation. However, closed-form solutions of the RTE are often not possible; for some geometries, the diffusion approximation can be used to simplify the RTE, although this, in turn, introduces many inaccuracies, especially near sources and boundaries. In contrast, Monte Carlo simulations can be made arbitrarily accurate by increasing the number of photons traced. For example, see the movie, where a Monte Carlo simulation of a pencil beam incident on a semi-infinite medium models both the initial ballistic photon flow and the later diffuse propagation.

In numerical analysis, the quasi-Monte Carlo method is a method for numerical integration and solving some other problems using low-discrepancy sequences. This is in contrast to the regular Monte Carlo method or Monte Carlo integration, which are based on sequences of pseudorandom numbers.

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It is often used when the search space is discrete. For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms such as gradient descent, Branch and Bound.

Umbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977. It is a particular physical application of the more general importance sampling in statistics.

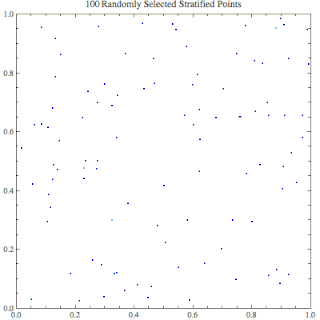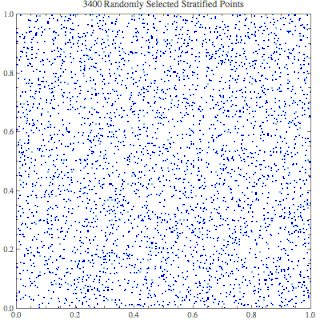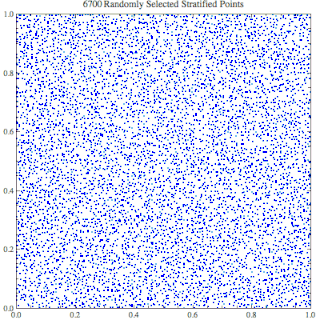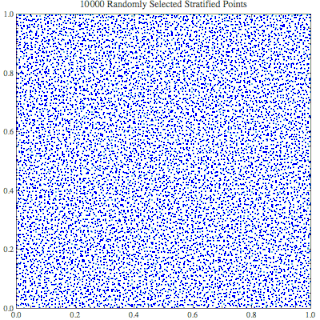
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given simulation or computational effort. Every output random variable from the simulation is associated with a variance which limits the precision of the simulation results. In order to make a simulation statistically efficient, i.e., to obtain a greater precision and smaller confidence intervals for the output random variable of interest, variance reduction techniques can be used. The main ones are common random numbers, antithetic variates, control variates, importance sampling, stratified sampling, moment matching, conditional Monte Carlo and quasi random variables. For simulation with black-box models subset simulation and line sampling can also be used. Under these headings are a variety of specialized techniques; for example, particle transport simulations make extensive use of "weight windows" and "splitting/Russian roulette" techniques, which are a form of importance sampling.