 W
WA number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called numerals; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any number using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels, for ordering, and for codes. In common usage, a numeral is not clearly distinguished from the number that it represents.
 W
WThe atomic number or proton number of a chemical element is the number of protons found in the nucleus of every atom of that element. The atomic number uniquely identifies a chemical element. It is identical to the charge number of the nucleus. In an uncharged atom, the atomic number is also equal to the number of electrons.
 W
WThe E series is a system of preferred numbers derived for use in electronic components. It consists of the E3, E6, E12, E24, E48, E96 and E192 series, where the number after the 'E' designates the quantity of value "steps" in each series. Although it is theoretically possible to produce components of any value, in practice the need for inventory simplification has led the industry to settle on the E series for resistors, capacitors, inductors, and zener diodes. Other types of electrical components are either specified by the Renard series or are defined in relevant product standards.
 W
WA fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A common, vulgar, or simple fraction consists of a numerator displayed above a line, and a non-zero denominator, displayed below that line. Numerators and denominators are also used in fractions that are not common, including compound fractions, complex fractions, and mixed numerals.
 W
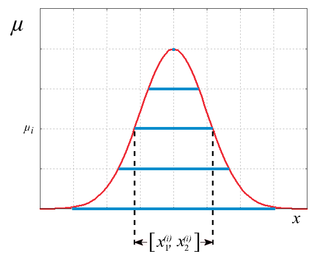
WA fuzzy number is a generalization of a regular, real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function. A fuzzy number is thus a special case of a convex, normalized fuzzy set of the real line. Just like Fuzzy logic is an extension of Boolean logic, fuzzy numbers are an extension of real numbers. Calculations with fuzzy numbers allow the incorporation of uncertainty on parameters, properties, geometry, initial conditions, etc. The arithmetic calculations on fuzzy numbers are implemented using fuzzy arithmetic operations, which can be done by two different approaches: (1) interval arithmetic approach; and (2) the extension principle approach.
 W
WAn illegal number is a number that represents information which is illegal to possess, utter, propagate, or otherwise transmit in some legal jurisdiction. Any piece of digital information is representable as a number; consequently, if communicating a specific set of information is illegal in some way, then the number may be illegal as well.
 W
WIn mathematics, a negative number is a real number that is less than zero. Negative numbers represent opposites. If positive represents a movement to the right, negative represents a movement to the left. If positive represents above sea level, then negative represents below sea level. If positive represents a deposit, negative represents a withdrawal. They are often used to represent the magnitude of a loss or deficiency. A debt that is owed may be thought of as a negative asset, a decrease in some quantity may be thought of as a negative increase. If a quantity may have either of two opposite senses, then one may choose to distinguish between those senses—perhaps arbitrarily—as positive and negative. Negative numbers are used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature. The laws of arithmetic for negative numbers ensure that the common sense idea of an opposite is reflected in arithmetic. For example, −(−3) = 3 because the opposite of an opposite is the original value.
 W
WIn mathematics, the concept of sign originates from the property that every real number is either positive, negative or zero. Depending on local conventions, zero is either considered as being neither a positive number, nor a negative number, or as belonging to both negative and positive numbers. Whenever not specifically mentioned, this article adheres to the first convention.
 W
WThe tables below list all of the divisors of the numbers 1 to 1000.