 W
WThe 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival. Danish computer scientist Peter Bro Miltersen first proposed the problem in 2003.
 W
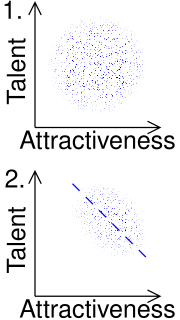
WBerkson's paradox, also known as Berkson's bias, collider bias or Berkson's fallacy, is a result in conditional probability and statistics which is often found to be counterintuitive, and hence a veridical paradox. It is a complicating factor arising in statistical tests of proportions. Specifically, it arises when there is an ascertainment bias inherent in a study design. The effect is related to the explaining away phenomenon in Bayesian networks, and conditioning on a collider in graphical models.
 W
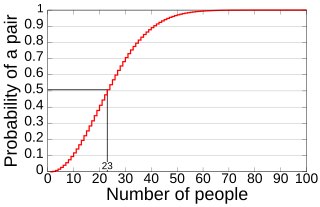
WIn probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367. However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people. These conclusions are based on the assumption that each day of the year is equally probable for a birthday.
 W
WThe two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle, or paradox in logic, probability, and recreational mathematics. It is of special interest in decision theory, and for the Bayesian interpretation of probability theory. Historically, it arose as a variant of the necktie paradox. The problem typically is introduced by formulating a hypothetical challenge of the following type:You are given two indistinguishable envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?
 W
WThe Monty Hall problem is a brain teaser, in the form of a probability puzzle, loosely based on the American television game show Let's Make a Deal and named after its original host, Monty Hall. The problem was originally posed in a letter by Steve Selvin to the American Statistician in 1975. It became famous as a question from a reader's letter quoted in Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990:Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
 W
WThe necktie paradox is a puzzle or paradox within the subjectivistic interpretation of probability theory, in which two men wager over whose necktie is cheapest, with the owner of the more expensive tie giving it to the other man. Both men reason that they stand to win more than they would lose, in such a bet. The necktie paradox is a variation of the two-envelope paradox.
 W
WSimpson's paradox, which also goes by several other names, is a phenomenon in probability and statistics, in which a trend appears in several different groups of data but disappears or reverses when these groups are combined. This result is often encountered in social-science and medical-science statistics and is particularly problematic when frequency data is unduly given causal interpretations. The paradox can be resolved when causal relations are appropriately addressed in the statistical modeling. It is also referred to as Simpson's reversal, Yule–Simpson effect, amalgamation paradox, or reversal paradox.
 W
WThe St. Petersburg paradox or St. Petersburg lottery is a paradox related to probability and decision theory in economics. It is based on a theoretical lottery game that leads to a random variable with infinite expected value but nevertheless seems to be worth only a very small amount to the participants. The St. Petersburg paradox is a situation where a naive decision criterion which takes only the expected value into account predicts a course of action that presumably no actual person would be willing to take. Several resolutions to the paradox have been proposed.
 W
WThe two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle, or paradox in logic, probability, and recreational mathematics. It is of special interest in decision theory, and for the Bayesian interpretation of probability theory. Historically, it arose as a variant of the necktie paradox. The problem typically is introduced by formulating a hypothetical challenge of the following type:You are given two indistinguishable envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?