 W
WAMPL is an algebraic modeling language to describe and solve high-complexity problems for large-scale mathematical computing . It was developed by Robert Fourer, David Gay, and Brian Kernighan at Bell Laboratories. AMPL supports dozens of solvers, both open source and commercial software, including CBC, CPLEX, FortMP, Gurobi, MINOS, IPOPT, SNOPT, KNITRO, and LGO. Problems are passed to solvers as nl files. AMPL is used by more than 100 corporate clients, and by government agencies and academic institutions.
 W
W"The Chemical Basis of Morphogenesis" is an article that the English mathematician Alan Turing wrote in 1952. It describes how patterns in nature, such as stripes and spirals, can arise naturally from a homogeneous, uniform state. The theory, which can be called a reaction–diffusion theory of morphogenesis, has become a basic model in theoretical biology. Such patterns have come to be known as Turing patterns. For example, it has been postulated that the protein VEGFC can form Turing patterns to govern the formation of lymphatic vessels in the zebrafish embryo.
 W
WA complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, social and economic organizations, an ecosystem, a living cell, and ultimately the entire universe.
 W
WExponential growth is a specific way that a quantity may increase over time. It occurs when the instantaneous rate of change of a quantity with respect to time is proportional to the quantity itself. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent.
 W
WThe forward problem of electrocardiology is a computational and mathematical approach to study the electrical activity of the heart through the body surface. The principal aim of this study is to computationally reproduce an electrocardiogram (ECG), which has important clinical relevance to define cardiac pathologies such as ischemia and infarction, or to test pharmaceutical intervention. Given their important functionalities and the relative small invasiveness, the electrocardiography techniques are used quite often as clinical diagnostic tests. Thus, it is natural to proceed to computationally reproduce an ECG, which means to mathematically model the cardiac behaviour inside the body.
 W
WThe generalized logistic function or curve, also known as Richards' curve, originally developed for growth modelling, is an extension of the logistic or sigmoid functions, allowing for more flexible S-shaped curves:
 W
WGlobal cascades models are a class of models aiming to model large and rare cascades that are triggered by exogenous perturbations which are relatively small compared with the size of the system. The phenomenon occurs ubiquitously in various systems, like information cascades in social systems, stock market crashes in economic systems, and cascading failure in physics infrastructure networks. The models capture some essential properties of such phenomenon.
 W
WInverse modeling is a mathematical technique where the objective is to determine the physical properties of the subsurface of an earth region that has produced a given seismogram. Cooke and Schneider (1983) defined it as calculation of the earth's structure and physical parameters from some set of observed seismic data. The underlying assumption in this method is that the collected seismic data are from an earth structure that matches the cross-section computed from the inversion algorithm. Some common earth properties that are inverted for include acoustic velocity, formation and fluid densities, acoustic impedance, Poisson's ratio, formation compressibility, shear rigidity, porosity, and fluid saturation.
 W
WThe Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
 W
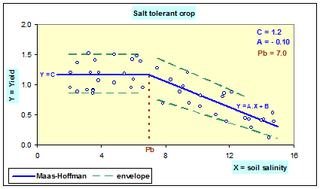
WThe Maas–Hoffman model is a mathematical tool to characterize the relation between crop production and soil salinity. It describes the crop response by a broken line of which the first part is horizontal and the second is sloping downward. The breakpoint (Pb) or threshold is also called tolerance because up to that point the yield is unaffected by the salinity, so the salt is tolerated, while at greater salinity values the crops are affected negatively and the yield goes down.
 W
WMicroscale models form a broad class of computational models that simulate fine-scale details, in contrast with macroscale models, which amalgamate details into select categories. Microscale and macroscale models can be used together to understand different aspects of the same problem.
 W
WReaction–diffusion systems are mathematical models which correspond to several physical phenomena. The most common is the change in space and time of the concentration of one or more chemical substances: local chemical reactions in which the substances are transformed into each other, and diffusion which causes the substances to spread out over a surface in space.
 W
WSecondary electro-spray ionization (SESI) is an ambient ionization technique for the analysis of trace concentrations of vapors, where a nano-electrospray produces charging agents that collide with the analyte molecules directly in gas-phase. In the subsequent reaction, the charge is transferred and vapors get ionized, most molecules get protonated and deprotonated. SESI works in combination with mass spectrometry or ion-mobility spectrometry.
 W
WThe Seshat: Global History Databank is an international scientific research project of the nonprofit Evolution Institute. Founded in 2011, the Seshat: Global History Databank gathers data into a single, large database that can be used to test scientific hypotheses. The Databank consults directly with expert scholars to code what historical societies and their environments were like in the form of accessible datapoints and thus forms a digital storehouse for data on the political and social organization of all human groups from the early modern back to the ancient and neolithic periods. The organizers of this research project contend that the mass of data then can be used to test a variety of competing hypotheses about the rise and fall of large-scale societies around the globe which may help science provide answers to global problems.
 W
WSimulink is a MATLAB-based graphical programming environment for modeling, simulating and analyzing multidomain dynamical systems. Its primary interface is a graphical block diagramming tool and a customizable set of block libraries. It offers tight integration with the rest of the MATLAB environment and can either drive MATLAB or be scripted from it. Simulink is widely used in automatic control and digital signal processing for multidomain simulation and model-based design.
 W
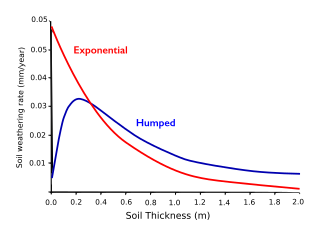
WSoil production function refers to the rate of bedrock weathering into soil as a function of soil thickness.
 W
WThe ten-ray model is a model applied to the transmissions in the urban area, to generate a model of ten rays typically four rays more are added to the six rays model, these are ; This incorporate paths from one to three reflections: specifically, there is the LOS, GR, SW, DW, TW, WG and GW. Where each one of the paths bounces on both sides of the wall.
 W
WThe theta model, or Ermentrout–Kopell canonical model, is a biological neuron model originally developed to model neurons in the animal Aplysia, and later used in various fields of computational neuroscience. The model is particularly well suited to describe neuron bursting, which are rapid oscillations in the membrane potential of a neuron interrupted by periods of relatively little oscillation. Bursts are often found in neurons responsible for controlling and maintaining steady rhythms. For example, breathing is controlled by a small network of bursting neurons in the brain stem. Of the three main classes of bursting neurons, the theta model describes parabolic bursting. Parabolic bursting is characterized by a series of bursts that are regulated by a slower external oscillation. This slow oscillation changes the frequency of the faster oscillation so that the frequency curve of the burst pattern resembles a parabola.
 W
WThe English mathematician Alan Turing introduced a concept, which came to be known as a Turing pattern, in a 1952 paper entitled "The Chemical Basis of Morphogenesis". This foundational paper describes how patterns in nature, such as stripes and spots, can arise naturally and autonomously from a homogeneous, uniform state. In his classic paper, Turing examined the behaviour of a system in which two diffusible substances interact with each other, and found that such a system is able to generate a spatially periodic pattern even from a random or almost uniform initial condition. Turing hypothesized that the resulting wavelike patterns are the chemical basis of morphogenesis. Turing patterning is often found in combination with others: vertebrate limb development is one of the many phenotypes exhibiting Turing overlapped with a complementary pattern.
 W
WThe van Genuchten–Gupta model is an inverted S-curve applicable to crop yield and soil salinity relations.
 W
WVflo is a commercially available, physics-based distributed hydrologic model generated by Vieux & Associates, Inc. Vflo uses radar rainfall data for hydrologic input to simulate distributed runoff. Vflo employs GIS maps for parameterization via a desktop interface. The model is suited for distributed hydrologic forecasting in post-analysis and in continuous operations. Vflo output is in the form of hydrographs at selected drainage network grids, as well as distributed runoff maps covering the watershed. Model applications include civil infrastructure operations and maintenance, stormwater prediction and emergency management, continuous and short-term surface water runoff, recharge estimation, soil moisture monitoring, land use planning, water quality monitoring, and water resources management.
 W
WThe von Bertalanffy growth function (VBGF), or von Bertalanffy curve, is a type of growth curve model for a time series and is named after Ludwig von Bertalanffy. It is a special case of the generalised logistic function. The growth curve is used to model mean length from age in animals. The function is commonly applied in ecology to model fish growth.
 W
WIn computational science, wildfire modeling is concerned with numerical simulation of wildland fires in order to understand and predict fire behavior. Wildfire modeling can ultimately aid wildland fire suppression, namely increase safety of firefighters and the public, reduce risk, and minimize damage. Wildfire modeling can also aid in protecting ecosystems, watersheds, and air quality.