 W
WIn cellular automata such as Conway's Game of Life, a breeder is a pattern that exhibits quadratic growth, by generating multiple copies of a secondary pattern, each of which then generates multiple copies of a tertiary pattern.
 W
WIn a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
 W
WThe glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1969, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of one cell every four generations, or . The glider is often produced from randomly generated starting configurations. John Conway remarked that he wished he hadn't called it the glider. The game was developed before the widespread use of interactive computers, and after seeing it animated, he feels the glider looks more like an ant walking across the plane.
 W
WIn a cellular automaton, a gun is a pattern with a main part that repeats periodically, like an oscillator, and that also periodically emits spaceships. There are then two periods that may be considered: the period of the spaceship output, and the period of the gun itself, which is necessarily a multiple of the spaceship output's period. A gun whose period is larger than the period of the output is a pseudoperiod gun.
 W
WIn cellular automata, a methuselah is a small "seed" pattern of initial live cells that take a large number of generations in order to stabilize. More specifically, Martin Gardner defines them as patterns of fewer than ten live cells which take longer than 50 generations to stabilize, although some patterns that are larger than ten cells have also been called methuselahs. Patterns must eventually stabilize to be considered methuselahs. The term comes from the Biblical Methuselah, who lived for 969 years.
 W
WA rake, in the lexicon of cellular automata, is a type of puffer train, which is an automaton that leaves behind a trail of debris. In the case of a rake, however, the debris left behind is a stream of spaceships, which are automata that "travel" by looping through a short series of iterations and end up in a new location after each cycle returns to the original configuration.
 W
WIn cellular automata such as Conway's Game of Life, a reflector is a pattern that can interact with a spaceship to change its direction of motion, without damage to the reflector pattern. In Life, many oscillators can reflect the glider; there also exist stable reflectors composed of still life patterns that, when they interact with a glider, reflect the glider and return to their stable state.
 W
WIn cellular automata, a replicator is a pattern that produces copies of itself.
 W
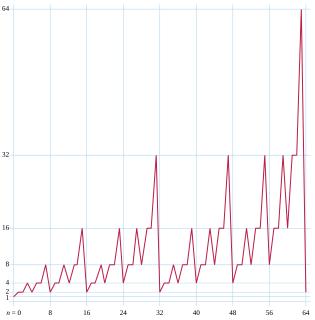
WIn a cellular automaton, a finite pattern is called a sawtooth if its population grows without bound but does not tend to infinity. In other words, a sawtooth is a pattern with population that reaches new heights infinitely often, but also infinitely often drops below some fixed value. Their name comes from the fact that their plot of population versus generation number looks roughly like an ever-increasing sawtooth wave.
 W
WThe Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
 W
WIn Conway's Game of Life and related cellular automata, a spacefiller is a pattern that spreads out indefinitely, eventually filling the entire space with a still life pattern. It typically consists of three components: stretchers that resemble spaceships at the four corners of the pattern, a growing boundary region along the edges of the pattern, and the still life in the interior pattern.
 W
WIn a cellular automaton, a finite pattern is called a spaceship if it reappears after a certain number of generations in the same orientation but in a different position. The smallest such number of generations is called the period of the spaceship.
 W
WIn Conway's Game of Life and similar cellular automaton rules, a spark is a small collection of live cells that appears at the edge of some larger pattern such as a spaceship or oscillator, then quickly dies off.
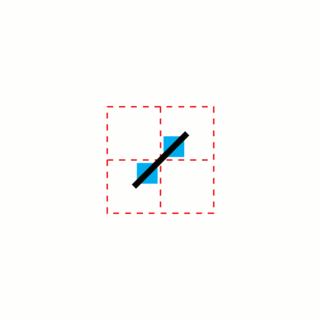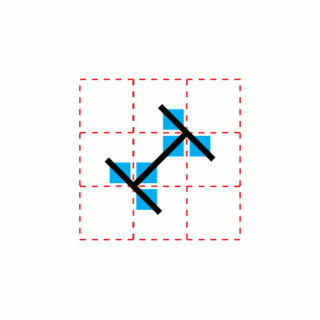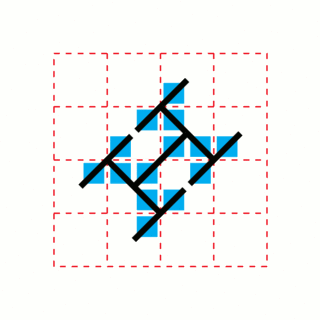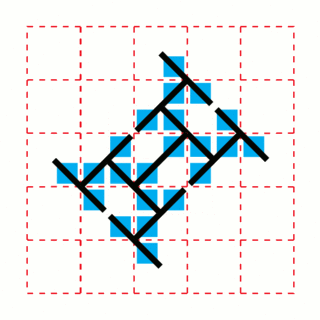 W
WIn geometry, the toothpick sequence is a sequence of 2-dimensional patterns which can be formed by repeatedly adding line segments ("toothpicks") to the previous pattern in the sequence.
 W
WJohn von Neumann's universal constructor is a self-replicating machine in a cellular automata (CA) environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in 1966 by Arthur W. Burks after von Neumann's death. While typically not as well known as von Neumann's other work, it is regarded as foundational for automata theory, complex systems, and artificial life. Indeed, Nobel Laureate Sydney Brenner considered Von Neumann's work on self-reproducing automata central to biological theory as well, allowing us to "discipline our thoughts about machines, both natural and artificial."