 W
WA tessellation or tiling of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.
 W
WIn geometry of the Euclidean plane, the 3-4-3-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, and dodecagons, arranged in two vertex configuration: 3.4.3.12 and 3.12.12.
 W
WIn geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.
 W
WIn geometry of the Euclidean plane, a 33344-33434 tiling is one of two of 20 2-uniform tilings of the Euclidean plane by regular polygons. They contains regular triangle and square faces, arranged in two vertex configuration: 3.3.3.4.4 and 3.3.4.3.4.
 W
WIn geometry, a shape is said to be anisohedral if it admits a tiling, but no such tiling is isohedral (tile-transitive); that is, in any tiling by that shape there are two tiles that are not equivalent under any symmetry of the tiling. A tiling by an anisohedral tile is referred to as an anisohedral tiling.
 W
WIn the mathematical theory of tessellations, the Conway criterion, named for the English mathematician John Horton Conway, is a fast way to identify many prototiles that tile the plane; it consists of the following requirements: The tile must be a closed topological disk with six consecutive points A, B, C, D, E, and F on the boundary such that:the boundary part from A to B is congruent by translation to the boundary part from E to D each of the boundary parts BC, CD, EF, and FA is centrosymmetric—that is, each one is congruent to itself when rotated by 180-degrees around its midpoint some of the six points may coincide but at least three of them must be distinct.
 W
WIn geometry, a corner-point grid is a tessellation of a Euclidean 3D volume where the base cell has 6 faces (hexahedron).
 W
WThe shrine of Darb-e Imam, located in the Dardasht quarter of Isfahan, Iran, is a funerary complex, with a cemetery, shrine structures, and courtyards belonging to different construction periods and styles. The first structures were built by Jalal al-Din Safarshah, during the Qara Qoyunlu reign in 1453.
 W
WIn geometry, an edge tessellation is a partition of the plane into non-overlapping polygons with the property that the reflection of any of these polygons across any of its edges is another polygon in the tessellation. All of the resulting polygons must be convex, and congruent to each other. There are eight possible edge tessellations in Euclidean geometry, but others exist in non-Euclidean geometry.
 W
WEuclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi.
 W
WIn applied mathematics, a Gilbert tessellation or random crack network is a mathematical model for the formation of mudcracks, needle-like crystals, and similar structures. It is named after Edgar Gilbert, who studied this model in 1967.
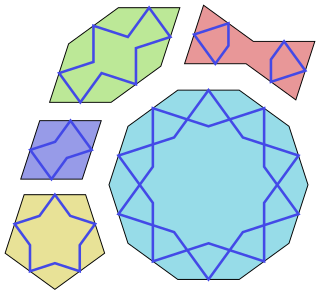 W
WGirih tiles are a set of five tiles that were used in the creation of Islamic geometric patterns using strapwork (girih) for decoration of buildings in Islamic architecture. They have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam shrine in Isfahan in Iran built in 1453.
 W
WHaeckelites are three-fold coordinated networks of carbon atoms generated by a periodic arrangement of pentagons, hexagons and heptagons. They were first proposed by Humberto and Mauricio Terrones and their colleagues in 2000. They were named in honour of Ernst Haeckel, whose diagrams of radiolaria contained similar structural features. They have not yet been synthesised in the laboratory, but have been the subject of a considerable amount of theoretical work.
 W
WA holmium–magnesium–zinc (Ho–Mg–Zn) quasicrystal is a quasicrystal made of an alloy of the three metals holmium, magnesium and zinc that has the shape of a regular dodecahedron, a Platonic solid with 12 five-sided faces. Unlike the similar pyritohedron shape of some cubic-system crystals such as pyrite, this quasicrystal has faces that are true regular pentagons.
 W
WIn spherical geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
 W
WIn geometry, Keller's conjecture is the conjecture that in any tiling of n-dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire (n − 1)-dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.
 W
WA k-uniform tiling is a tiling of tilings of the plane by convex regular polygons, connected edge-to-edge, with k types of vertices. The 1-uniform tiling include 3 regular tilings, and 8 semiregular tilings. A 1-uniform tiling can be defined by its vertex configuration. Higher k-uniform tilings are listed by their vertex figures, but are not generally uniquely identified this way.
 W
WIn geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.
 W
WIn the mathematical theory of tessellations, a prototile is one of the shapes of a tile in a tessellation.
 W
WThe quaquaversal tiling is a nonperiodic tiling of the euclidean 3-space introduced by John Conway and Charles Radin. The basic solid tiles are half prisms arranged in a pattern that relies essentially on their previous construct, the pinwheel tiling. The rotations relating these tiles belong to the group G(6,4) generated by two rotations of order 6 and 4 whose axes are perpendicular to each other. These rotations are dense in SO(3).
 W
WA quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical crystallographic restriction theorem, can possess only two-, three-, four-, and six-fold rotational symmetries, the Bragg diffraction pattern of quasicrystals shows sharp peaks with other symmetry orders—for instance, five-fold.
 W
WA regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes. Grids of this type appear on graph paper and may be used in finite element analysis, finite volume methods, finite difference methods, and in general for discretization of parameter spaces. Since the derivatives of field variables can be conveniently expressed as finite differences, structured grids mainly appear in finite difference methods. Unstructured grids offer more flexibility than structured grids and hence are very useful in finite element and finite volume methods.
 W
WIn the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.
 W
WA self-tiling tile set, or setiset, of order n is a set of n shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of n shapes. That is, the n shapes can be assembled in n different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for n = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by Lee Sallows in 2012, but the problem of finding such sets for n = 4 was asked decades previously by C. Dudley Langford, and examples for polyaboloes and polyominoes were previously published by Gardner.
 W
WIn mathematics, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.
 W
WSquaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.
 W
WSquaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.
 W
WIn geometry, a tetrad is four simply connected planar regions in the plane, each pair which share a finite portion of common boundary. It was named by Michael R. W. Buckley in 1975 in the Journal of Recreational Mathematics. A further question was proposed that became a puzzle, whether the 4 regions could be congruent, with or without holes, other enclosed regions.
 W
WTiling puzzles are puzzles involving two-dimensional packing problems in which a number of flat shapes have to be assembled into a larger given shape without overlaps. Some tiling puzzles ask you to dissect a given shape first and then rearrange the pieces into another shape. Other tiling puzzles ask you to dissect a given shape while fulfilling certain conditions. The two latter types of tiling puzzles are also called dissection puzzles.
 W
WThe Voderberg tiling is a mathematical spiral tiling, invented in 1936 by mathematician Heinz Voderberg (1911-1945). It is a monohedral tiling: it consists of only one shape that tessellates the plane with congruent copies of itself. In this case, the prototile is an elongated irregular nonagon, or nine-sided figure. The most interesting feature of this polygon is the fact that two copies of it can fully enclose a third one. E.g., the lowest purple nonagon is enclosed by two yellow ones, all three of identical shape. Before Voderberg's discovery, mathematicians had questioned whether this could be possible.