 W
WAndrica's conjecture is a conjecture regarding the gaps between prime numbers.
 W
WIn number theory, Firoozbakht’s conjecture is a conjecture about the distribution of prime numbers. It is named after the Iranian mathematician Farideh Firoozbakht from the University of Isfahan who stated it first in 1982.
 W
WGoldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even whole number greater than 2 is the sum of two prime numbers.
 W
WIn number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states thatEvery odd number greater than 5 can be expressed as the sum of three primes.
 W
WLegendre's constant is a mathematical constant occurring in a formula conjectured by Adrien-Marie Legendre to capture the asymptotic behavior of the prime-counting function . Its value is now known to be 1.
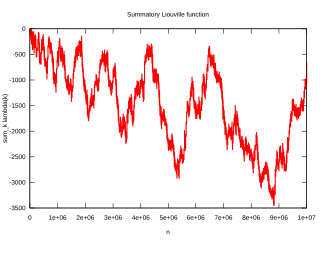 W
WIn number theory, the Pólya conjecture stated that "most" of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958 by C. Brian Haselgrove.
 W
WIn number theory, the second Hardy–Littlewood conjecture concerns the number of primes in intervals. Along with the first Hardy–Littlewood conjecture, the second Hardy–Littlewood conjecture was proposed by G. H. Hardy and John Edensor Littlewood in 1923.