 W
WThe abacus, also called a counting frame, is a calculating tool which has been used since ancient times. It was used in the ancient Near East, Europe, China, and Russia, centuries before the adoption of the Arabic numeral system. The exact origin of the abacus has not yet emerged. It consists of rows of movable beads, or similar objects, strung on a wire. They represent digits. One of the two numbers is set up, and the beads are manipulated to perform an operation such as addition, or even a square or cubic root.
 W
WCounting rods are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
 W
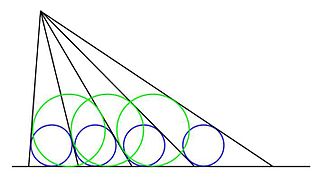
WIn geometry, the equal incircles theorem derives from a Japanese Sangaku, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal. In the illustration the equal blue circles define the spacing between the rays, as described.
 W
WIn geometry, the Japanese theorem states that no matter how one triangulates a cyclic polygon, the sum of inradii of triangles is constant.
 W
WIn geometry, the Japanese theorem states that the centers of the incircles of certain triangles inside a cyclic quadrilateral are vertices of a rectangle.
 W
WIn geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height.
 W
WSangaku or San Gaku are Japanese geometrical problems or theorems on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.
 W
WTian yuan shu is a Chinese system of algebra for polynomial equations. Some of the earliest existing writings were created in the 13th century during the Yuan dynasty. However, the tianyuanshu method was known much earlier, in the Song dynasty and possibly before.